Similar Figures Worksheet

Are you in search of a comprehensive and reliable worksheet to enhance your knowledge of similar figures? Look no further! This blog post is specifically designed to cater to the needs of students and individuals seeking a detailed understanding of entities and subjects related to similar figures.

  14 Images of Similar Figures Worksheet

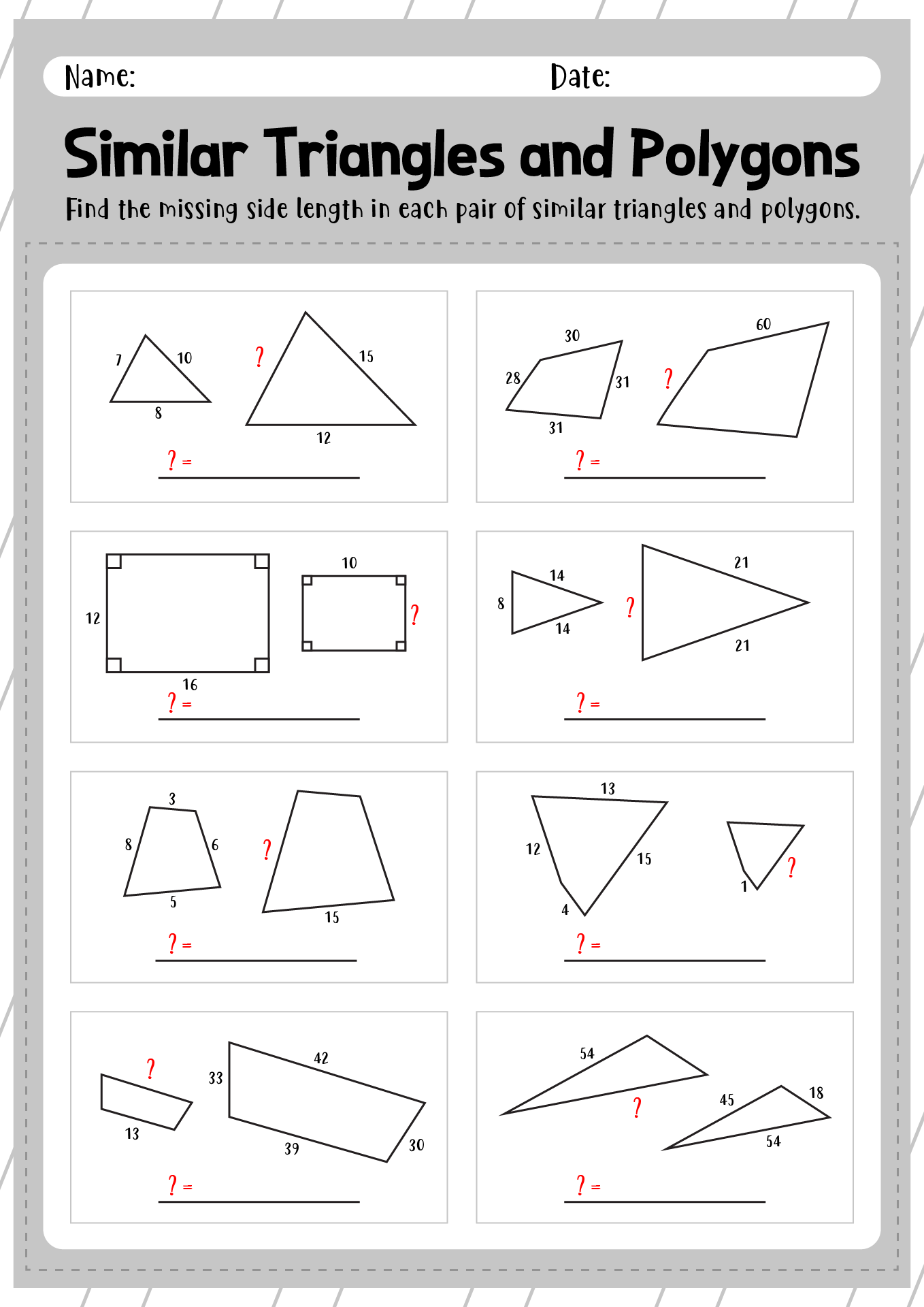
  Similar Triangles and Polygons Worksheet

---

  Similar and Congruent Figures Worksheet

---

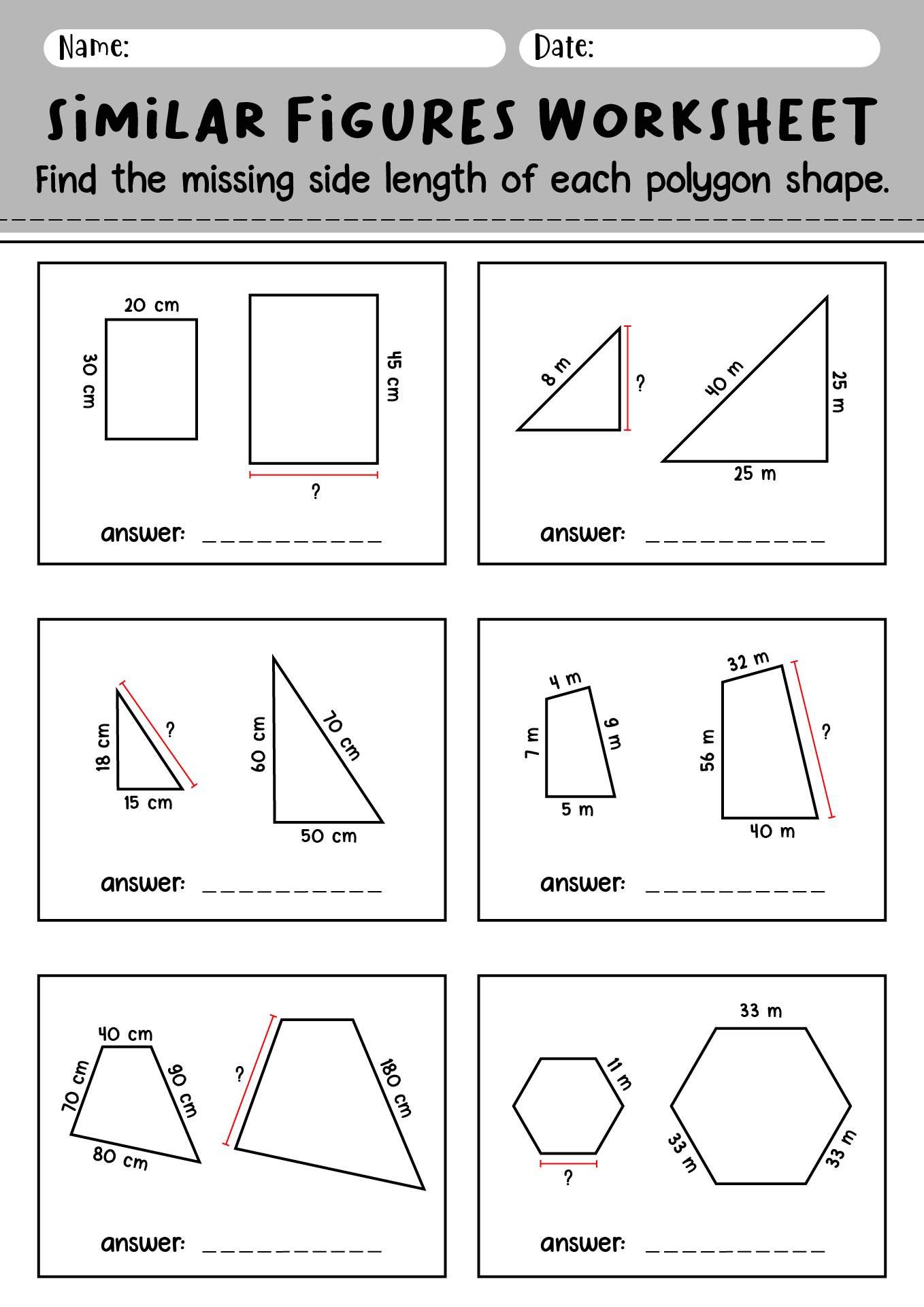
  Similar Figures and Proportions Worksheets

---

  Similar Figures Proportions Worksheet

---

  Similar Figures and Proportions Worksheets

---

  Similar Figures Proportions Worksheet

---

  Congruent and Similar Triangles Worksheet

---

  Similar Figures 7th Grade Worksheets

---

  Similar Polygons Worksheet

---

  Congruent and Similar Polygons Worksheets

---

  Similar Figures 7th Grade Worksheets

---

  Similar Polygons Worksheet

---

  Similar Figures Practice Sheet

---

  Geometry Similar Figures Exercises

---

What are similar figures?

Similar figures are geometric figures that have the same shape but are scaled differently in size. This means that the corresponding angles are equal, and the corresponding sides are proportional to each other. While the shapes may have different sizes, they have the same shape and maintain the same proportions.

What is the relationship between corresponding angles of similar figures?

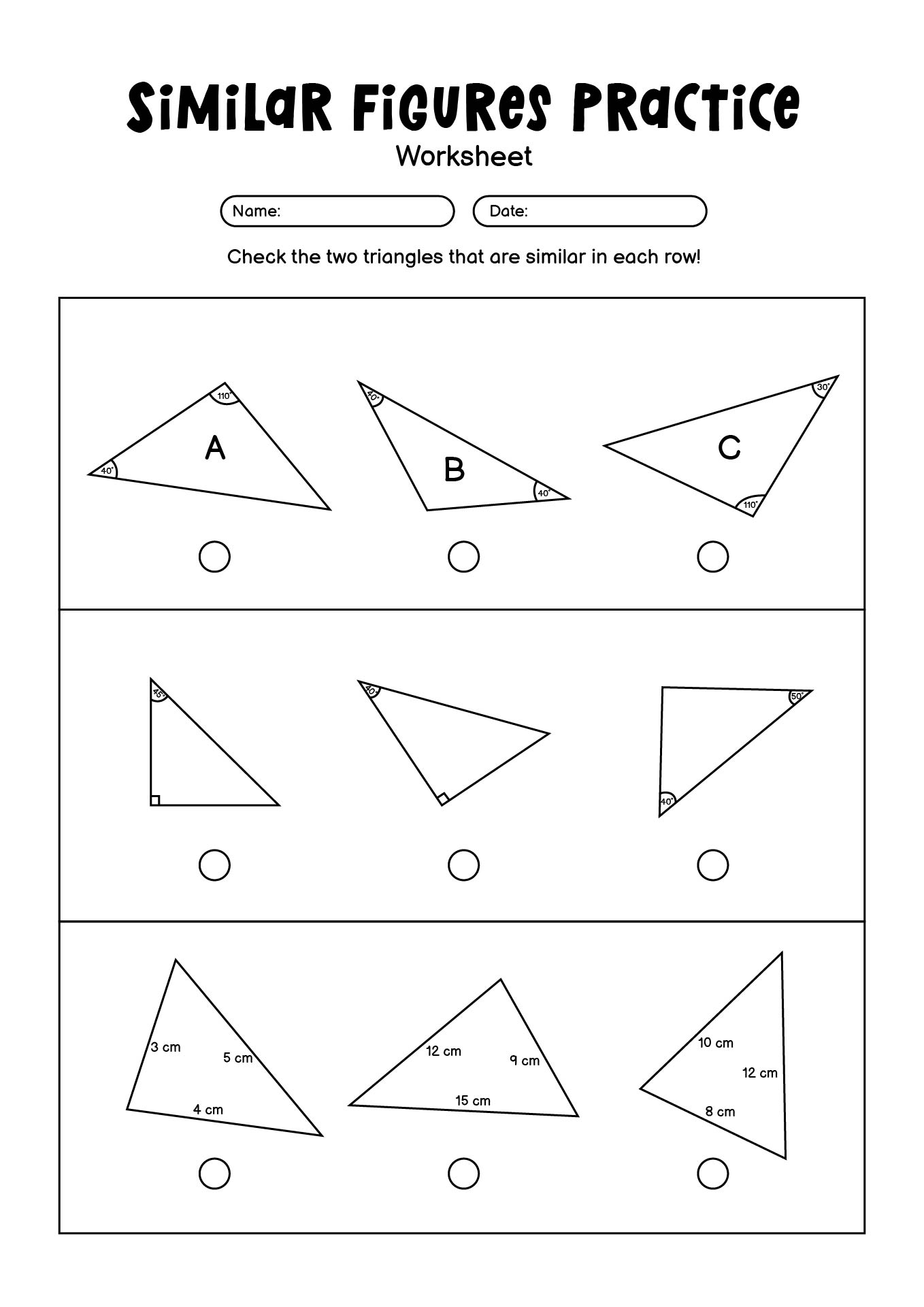
Corresponding angles of similar figures are congruent, meaning they have equal measures. In other words, when two figures are similar, the angles in the first figure will have the same measure as the corresponding angles in the second figure. This property is one of the key characteristics of similar figures and helps establish their geometric similarity.

What is the relationship between corresponding sides of similar figures?

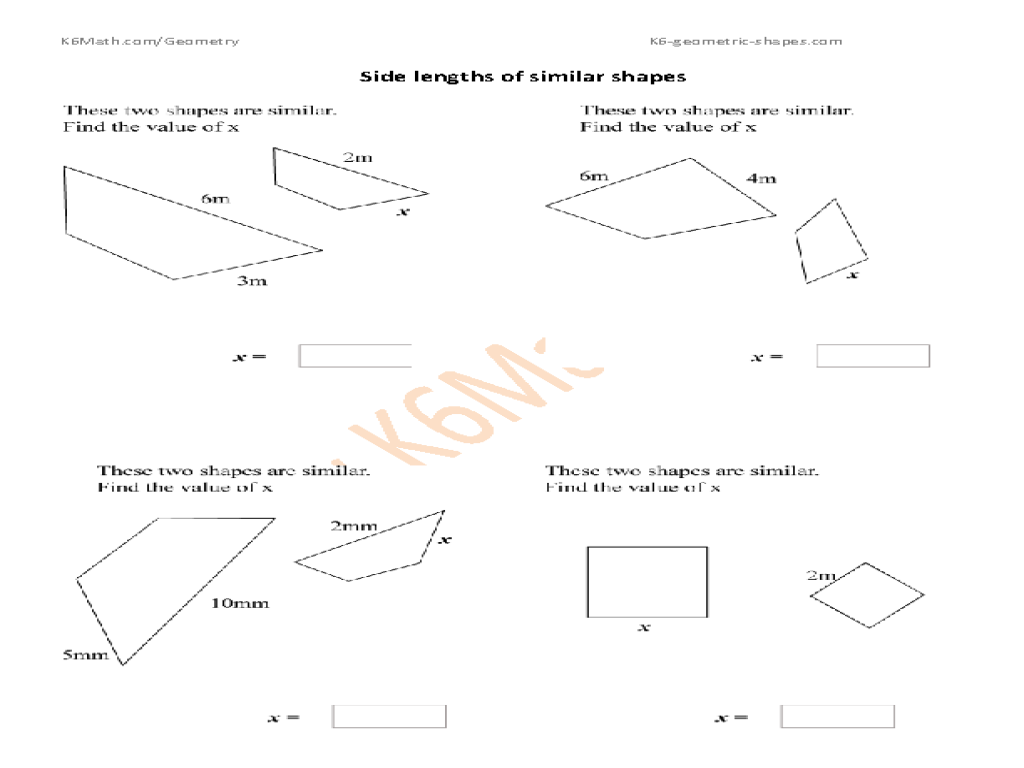
The relationship between corresponding sides of similar figures is that they are proportional. This means that the ratios of the lengths of corresponding sides are equal, which highlights the similarity between the two figures. This proportionality allows us to establish a scale factor that can be used to determine the length of any side in one figure based on the corresponding side in the other figure.

How can you determine if two figures are similar?

Two figures are considered similar if they have the same shape but different sizes. To determine if two figures are similar, you can check if their corresponding angles are equal and if their corresponding sides are in proportion to each other. In other words, if the ratios of the lengths of the sides of one figure to the other are equal, then the figures are similar.

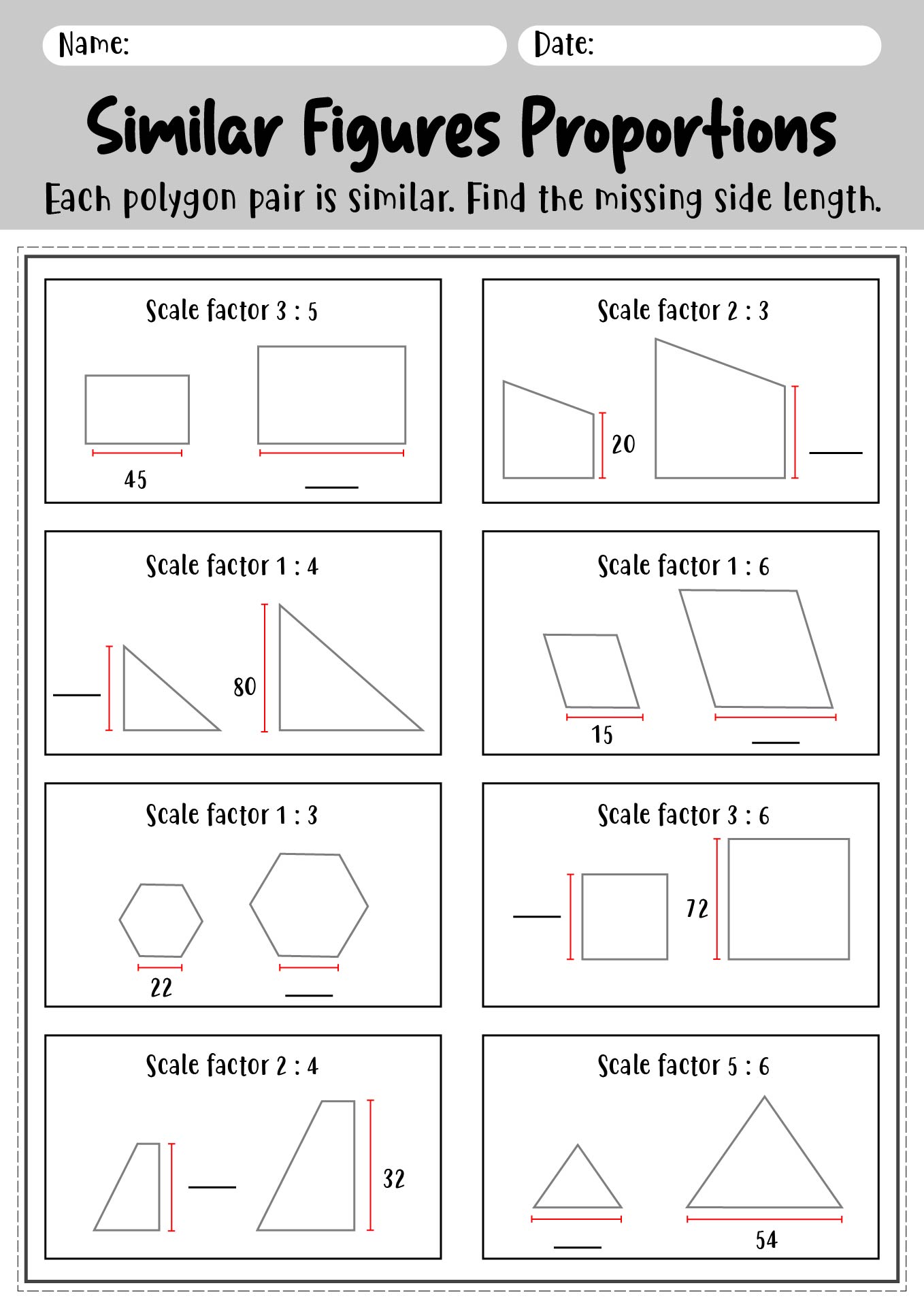
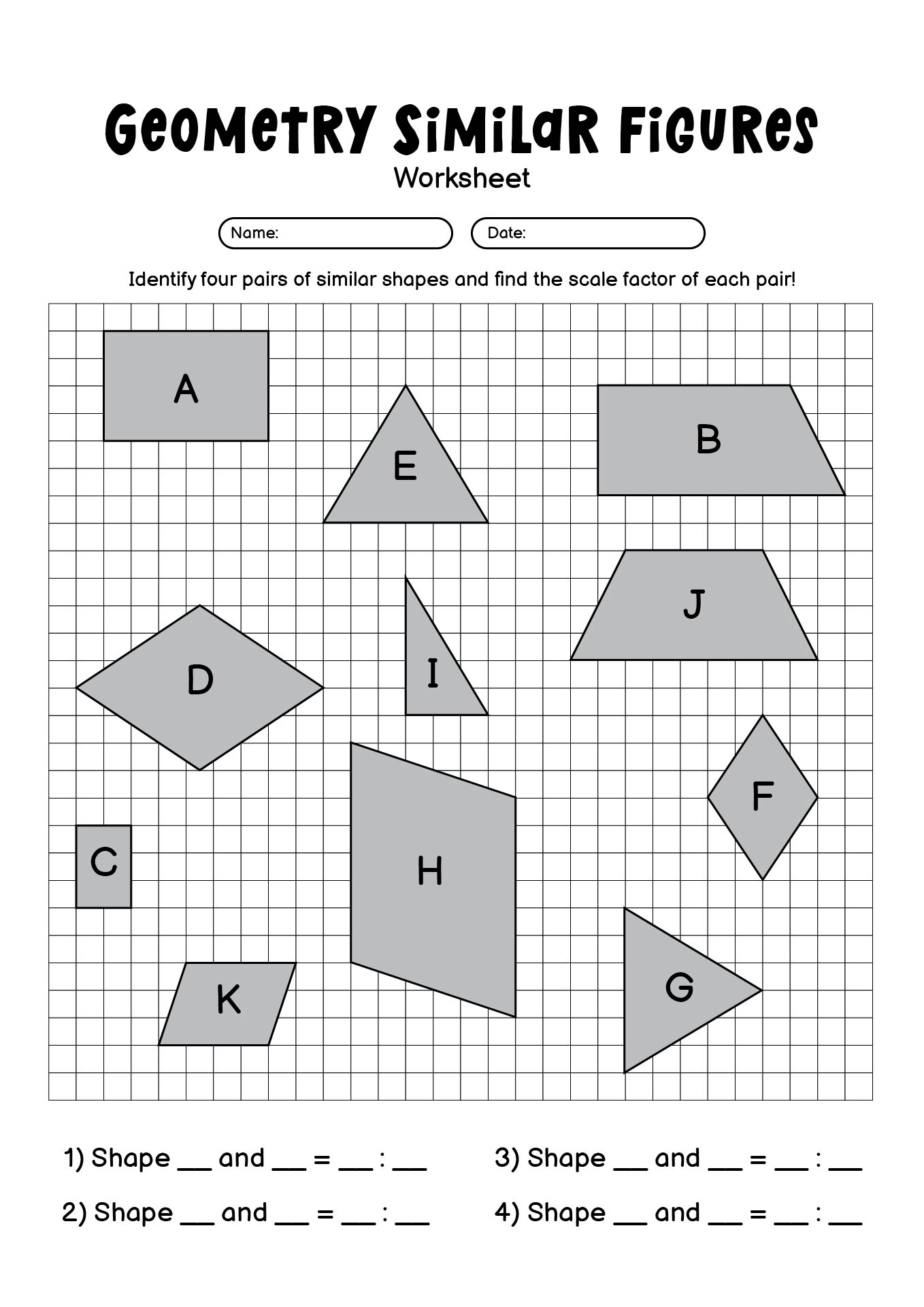
What is the scale factor between two similar figures?

The scale factor between two similar figures is the ratio of the lengths of corresponding sides. It is the factor by which each side of the smaller figure must be multiplied to obtain the corresponding side of the larger figure. This ratio remains constant for all pairs of corresponding sides in similar figures.

How does the scale factor affect the corresponding angles of similar figures?

The scale factor directly influences the corresponding angles of similar figures. When two figures are similar, their corresponding angles are congruent, meaning they have the same measure. When a figure is enlarged or reduced by a scale factor, the corresponding angles maintain their original relationship and remain equal to each other. Essentially, the scale factor does not change the measures of corresponding angles in similar figures.

How does the scale factor affect the corresponding sides of similar figures?

The scale factor affects the corresponding sides of similar figures by determining how their lengths relate to each other. When two figures are similar, their corresponding sides are in proportion to each other based on the scale factor. This means that if you multiply the length of a side in one figure by the scale factor, you will get the length of the corresponding side in the other similar figure. A scale factor greater than 1 will result in an enlargement of the figure, while a scale factor between 0 and 1 will result in a reduction in size.

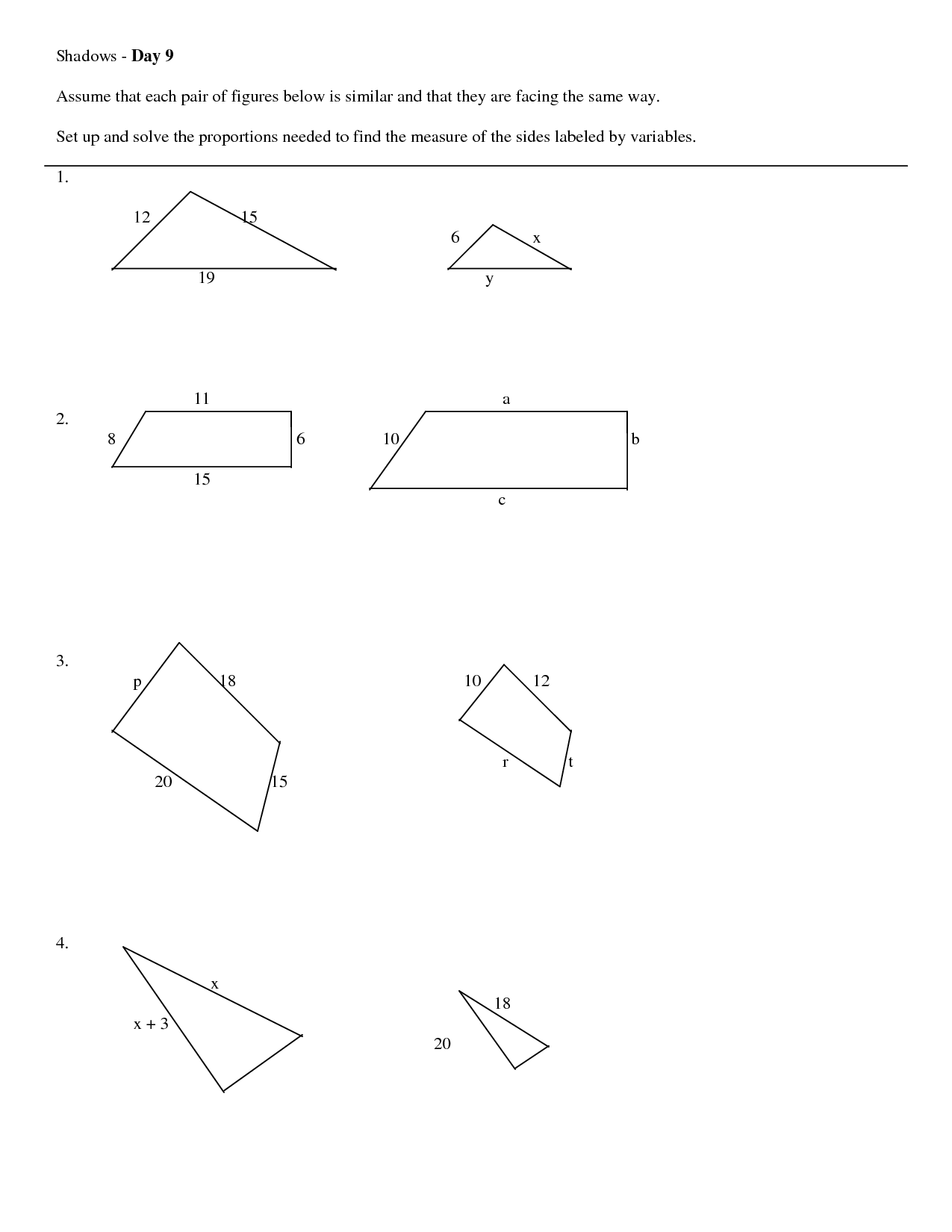
How can you find missing side lengths in similar figures using the scale factor?

To find missing side lengths in similar figures using the scale factor, you can set up a proportion between the corresponding sides of the two figures. The scale factor is the ratio of the length of a side in one figure to the length of the corresponding side in the other figure. By setting up a proportion with the known side lengths and the scale factor, you can solve for the missing side lengths by cross-multiplying and then isolating the variable.

How can you find missing angle measures in similar figures using the scale factor?

To find missing angle measures in similar figures using the scale factor, you can use the fact that corresponding angles in similar figures are congruent. First, identify corresponding angles in both figures. Then, set up a proportion using the measures of the known angles and the scale factor of the figures. Cross multiply and solve for the unknown angle measure. Remember that when two figures are similar, their corresponding angles are equal in measure.

Can you provide an example problem using similar figures and explain the solution?

Sure, here's an example problem using similar figures: If two triangles are similar and one triangle has a side length of 4cm while the corresponding side length on the other triangle is 8cm, what is the scale factor between the two triangles? The solution is to set up a proportion using the corresponding side lengths: 4/8 = x/1, where x represents the scale factor. Simplifying the proportion gives 0.5 = x/1, which means x = 0.5. Therefore, the scale factor between the two triangles is 0.5.