Classifying Triangles and Angles Worksheet

Are you a math teacher on the hunt for a comprehensive worksheet to help your students master the classification of triangles and angles? Look no further! We have designed a precise and informative worksheet that focuses on these specific topics to ensure your students fully understand the concepts and can confidently solve related problems.

  13 Images of Classifying Triangles And Angles Worksheet

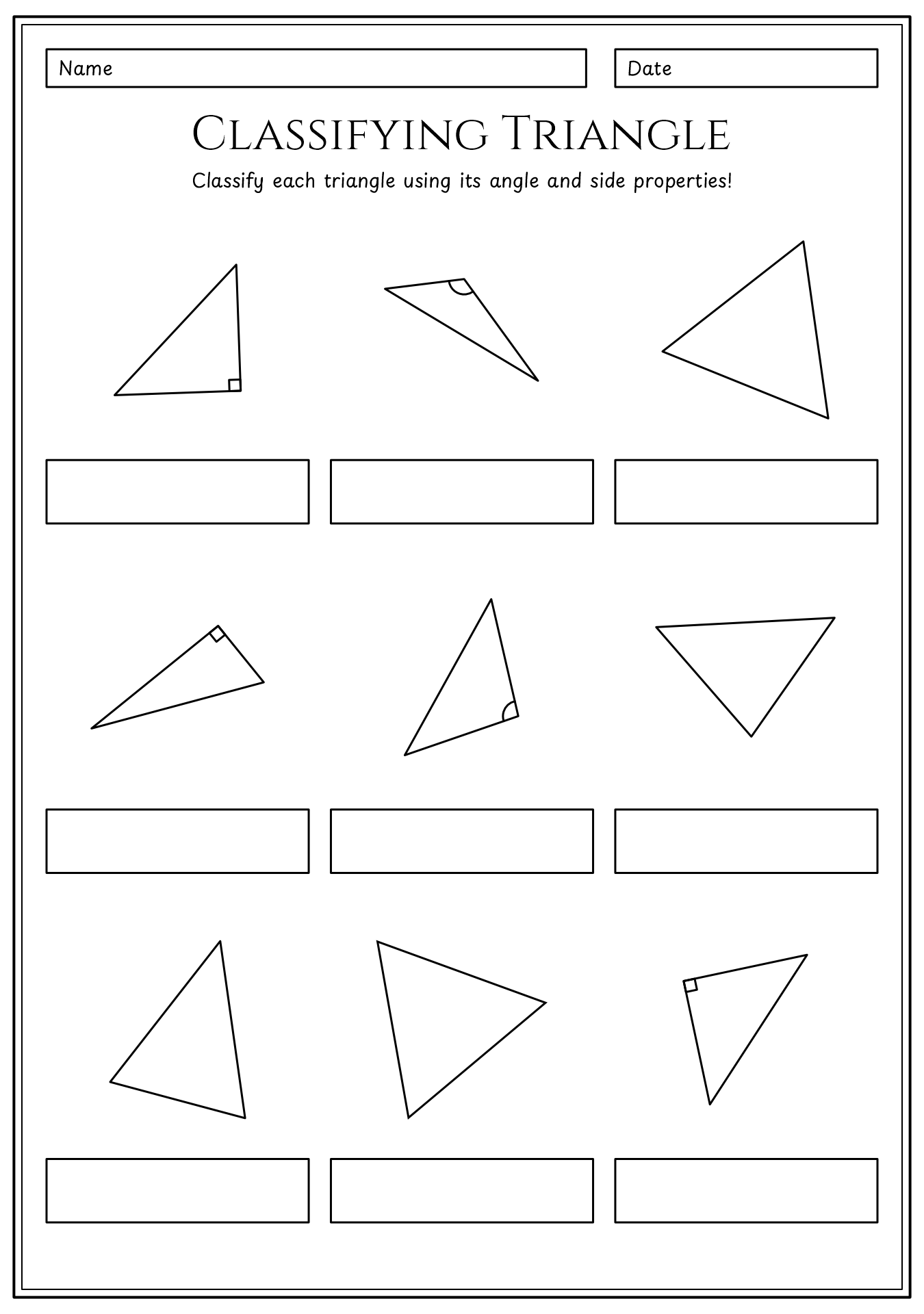
  Classifying Triangles by Angles Worksheet

---

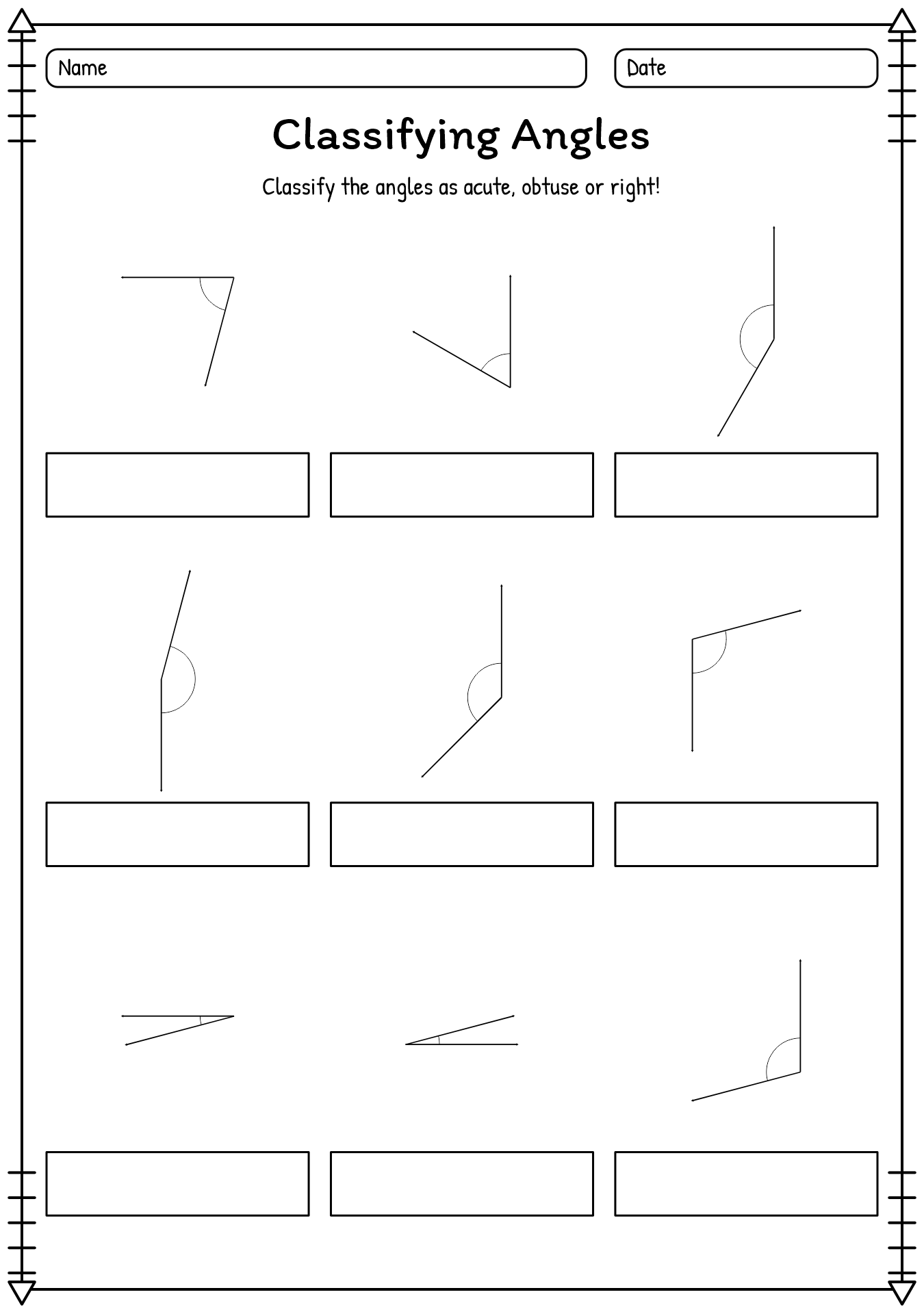
  Classifying Angles Worksheet

---

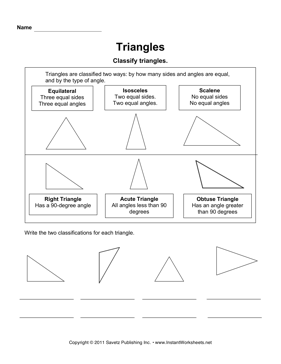
  Classifying Triangles Worksheet

---

  Classifying Triangles Worksheet

---

  Classifying Triangles Worksheet

---

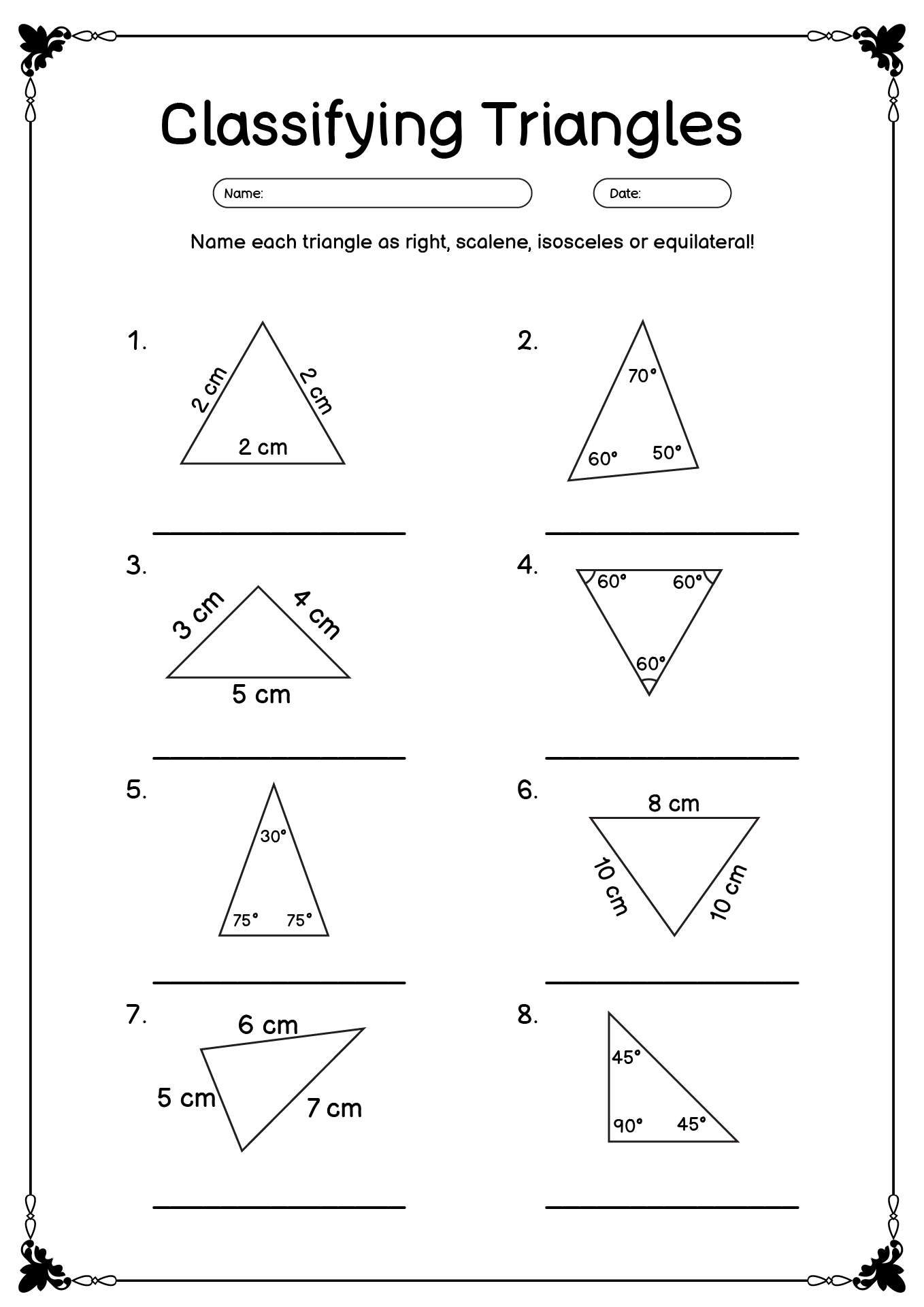
  Classifying Triangles by Sides and Angles

---

  Identifying Triangles Worksheets

---

  Acute Obtuse Right Angles Worksheet

---

  Triangles and Quadrilaterals Worksheet

---

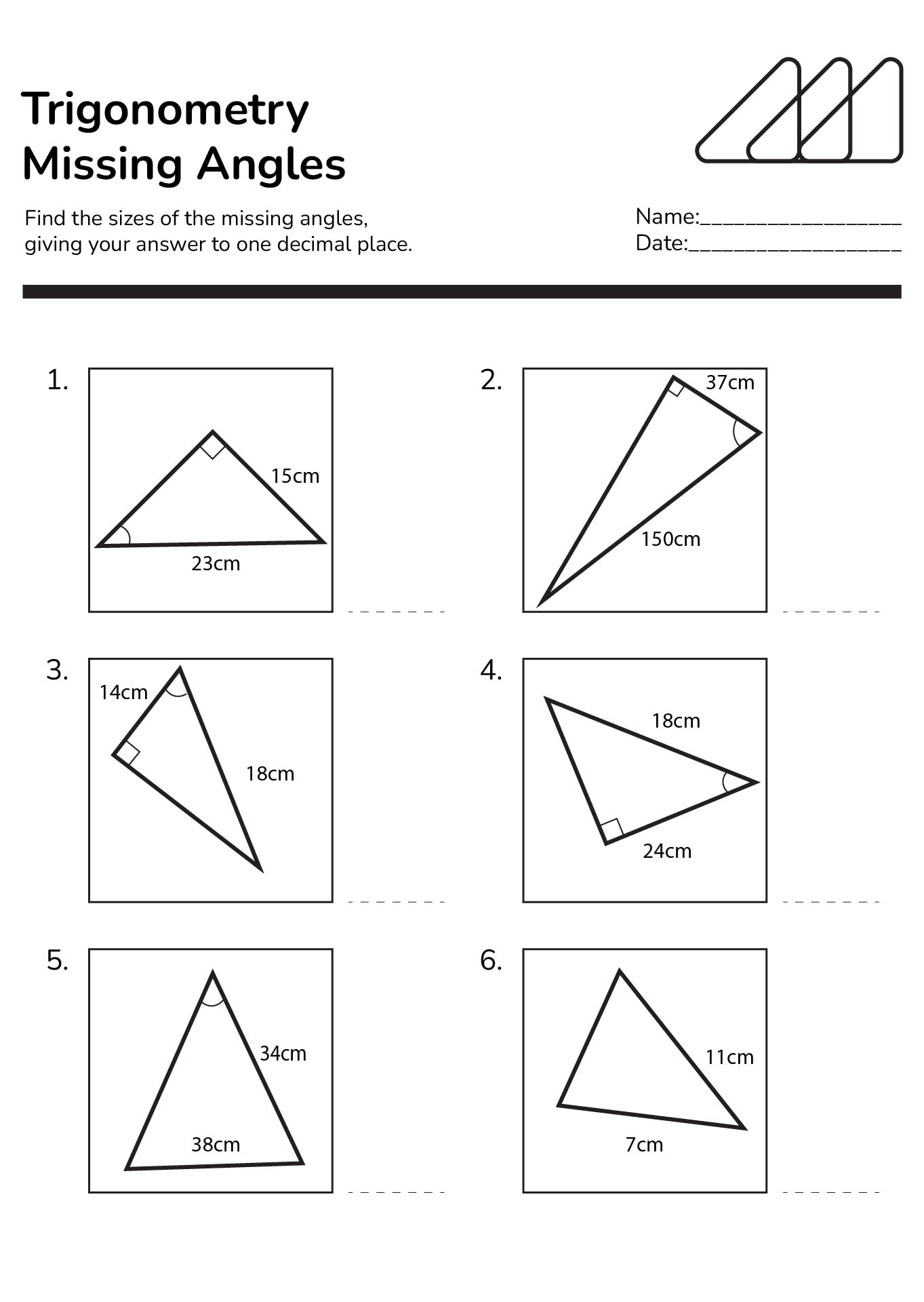
  Trig Right Triangle Missing Angles Worksheet

---

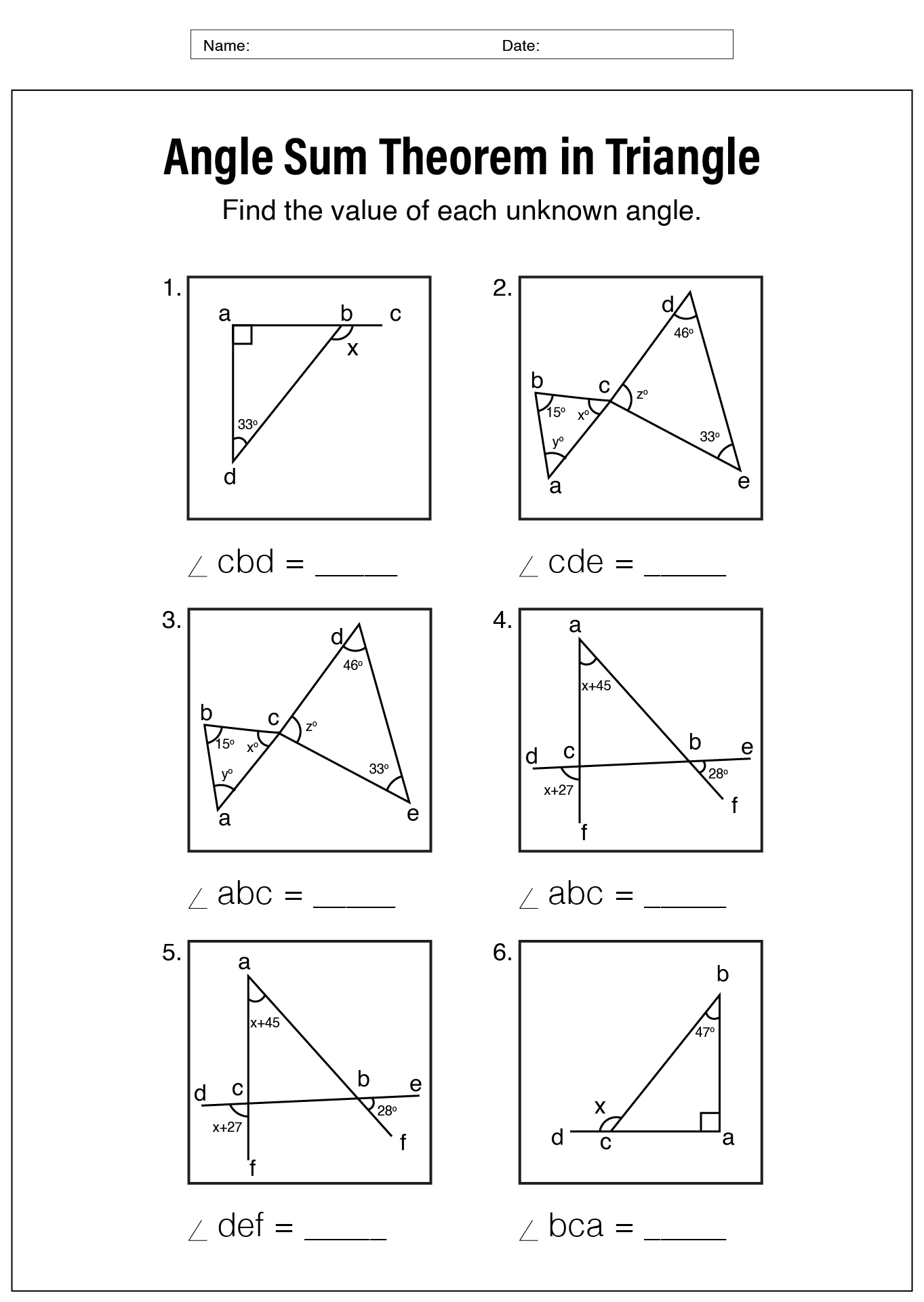
  Triangle Angle Sum Theorem Worksheet

---

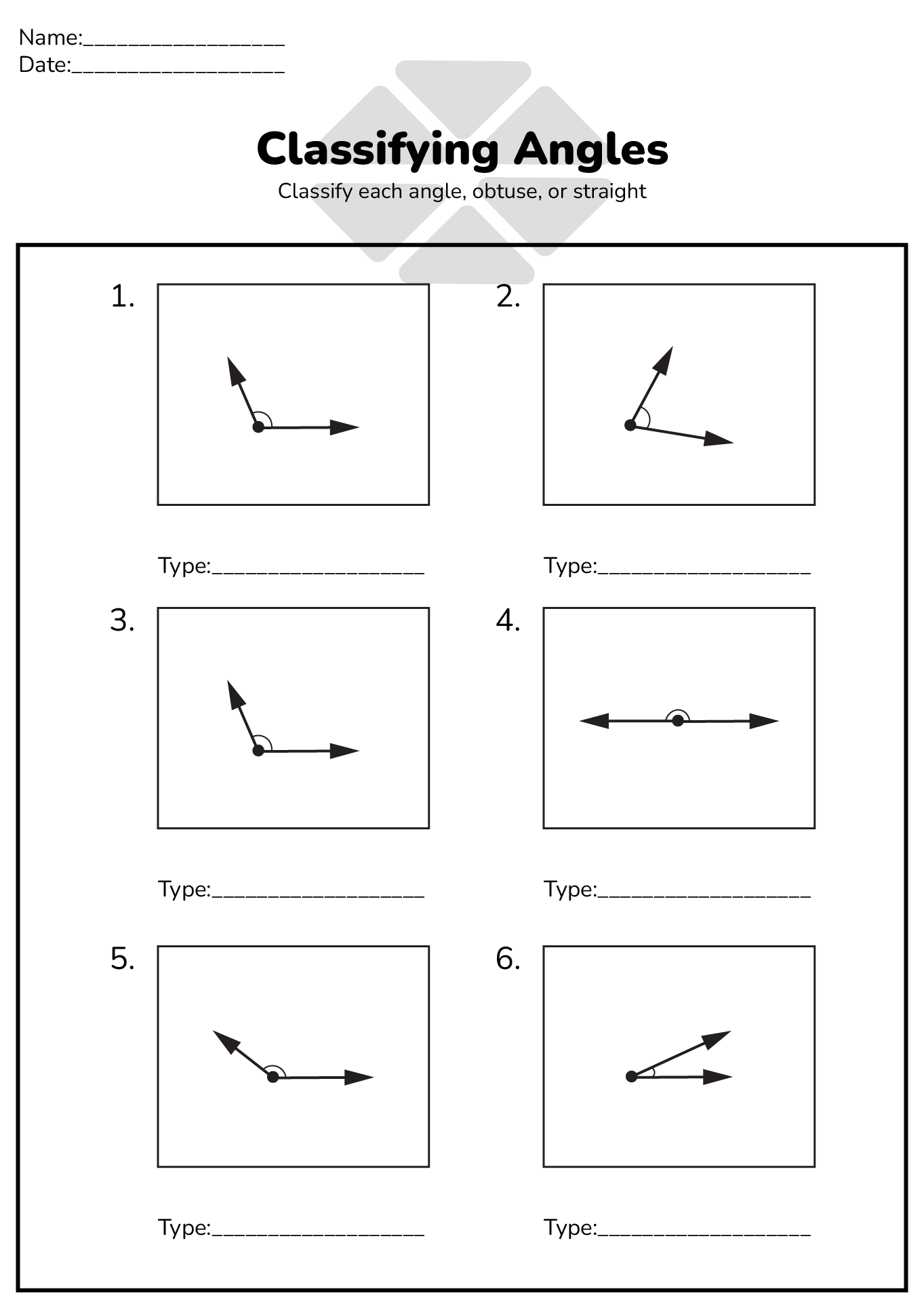
  Classifying Angles Worksheet

---

  Classifying Angles Geometry

---

Understanding the concepts of classifying triangles and angles is crucial, and our Classifying Triangles and Angles Worksheet can serve as an excellent resource for students to practice.

What are the different types of triangles based on their side lengths?

Triangles can be categorized based on their side lengths into three main types: scalene triangles (all three sides have different lengths), isosceles triangles (two sides have the same length), and equilateral triangles (all three sides have the same length).

How can you determine if a triangle is equilateral?

A triangle is considered equilateral if all three of its sides are of equal length. To determine if a triangle is equilateral, you can measure the lengths of its sides and compare them. If all three sides have the same length, then the triangle is equilateral.

What are isosceles triangles and how can you identify them?

Isosceles triangles are triangles that have two sides of equal length. You can identify an isosceles triangle by observing that two of its sides are the same length, which will also result in two of its angles being equal. This characteristic makes isosceles triangles unique and easy to distinguish from other types of triangles.

What is a scalene triangle and how is it different from other types of triangles?

A scalene triangle is a triangle with three different side lengths and three different angle measures. Unlike equilateral triangles with three equal sides and three equal angles, or isosceles triangles with at least two equal sides and two equal angles, a scalene triangle has no sides or angles that are equal. This makes it unique from other types of triangles due to its asymmetrical nature, where no two sides or angles are the same.

How are right triangles defined and what is their unique characteristic?

Right triangles are defined as triangles that have one 90-degree angle. The unique characteristic of right triangles is that they satisfy the Pythagorean theorem, which states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This relationship is fundamental in mathematics and geometry, making right triangles an essential concept in the study of geometry and trigonometry.

Can a triangle have more than one right angle? Explain.

No, a triangle cannot have more than one right angle. A right angle in a triangle measures 90 degrees, and the sum of the angles in any triangle is always 180 degrees. Therefore, if a triangle had more than one right angle, the sum of all the angles would exceed 180 degrees, which is not possible within the constraints of Euclidean geometry.

What are acute angles and how do they relate to triangles?

Acute angles are angles that measure less than 90 degrees. In a triangle, all three angles must add up to 180 degrees. Therefore, if one angle of a triangle is acute (less than 90 degrees), then the other two angles must also be acute in order for the sum to equal 180 degrees. This means that triangles with acute angles will always have all three angles less than 90 degrees.

Define obtuse angles and provide an example of an obtuse triangle.

An obtuse angle is an angle greater than 90 degrees but less than 180 degrees. An example of an obtuse triangle is a triangle with one obtuse angle, such as a triangle with angles measuring 30 degrees, 70 degrees, and 80 degrees.

What is the sum of the interior angles in a triangle?

The sum of the interior angles in a triangle is always 180 degrees.

Explain how you can classify triangles based on both their angles and side lengths.

Triangles can be classified based on both their angles and side lengths. In terms of angles, triangles can be classified as equiangular (all angles are equal), acute (all angles are less than 90 degrees), obtuse (one angle is greater than 90 degrees), or right (one angle is exactly 90 degrees). When it comes to side lengths, triangles can be categorized as equilateral (all sides are equal in length), isosceles (two sides are equal in length), scalene (no sides are equal in length). By considering both angle measurements and side lengths, a triangle can be classified with specificity based on these characteristics.