Solving Linear Equations Worksheet with Answers
Are you a math enthusiast searching for an effective tool to practice solving linear equations? Look no further! Our comprehensive solving linear equations worksheet with answers is designed to help students strengthen their skills in this fundamental math topic. With a focus on clear entity and subject, our worksheet allows learners to grasp the concept of linear equations effortlessly and master the necessary techniques for solving them accurately.
Table of Images 👆
- Algebra Solving Linear Equations Worksheets
- Algebra Solving Linear Equations Worksheets
- Solving Literal Equations Worksheet
- Solving Equations with Rational Expressions Worksheet
- Solving Linear Equations by Substitution Worksheet
- Solving Equations and Inequalities Worksheet
- Solving Equations Worksheets
- Solving Algebra Equations Worksheets
- Solving Two-Step Equations Worksheet Answers
- Two-Step Equations Worksheet
- Writing Linear Equations Worksheet Answer Key
- Linear Equations with Fractions Worksheet
- Algebra Literal Equations Worksheets Answers
- Absolute Value Inequalities Worksheets
- Literal Equations Worksheet Answer Key
- Solving Linear Systems by Substitution Worksheet
- Systems of Linear Equations Two Variables Worksheets
More Line Worksheets
Lines of Symmetry WorksheetsLine Drawing Art Worksheets
Drawing Contour Lines Worksheet
Contour Lines Topographic Map Worksheets
Rosa Parks Timeline Worksheet
Blank Printable Timeline Worksheets
What is the purpose of solving linear equations?
The purpose of solving linear equations is to find the values of the variables that satisfy the equation and make it true. This helps in finding solutions to real-world problems, understanding relationships between different variables, and making predictions based on the given information. Additionally, solving linear equations helps in simplifying complex problems and forming a foundation for more advanced mathematical concepts and problem-solving techniques.
What are the steps involved in solving a linear equation?
To solve a linear equation, you first simplify both sides by performing any necessary operations (such as combining like terms or distributing). Next, isolate the variable by moving constants to one side and the variable to the other side of the equation using inverse operations (addition, subtraction, multiplication, division). Then, solve for the variable by computing the final result. Finally, verify your solution by substituting it back into the original equation to ensure it satisfies the equality.
How can you determine if an equation has no solution?
You can determine if an equation has no solution if, after simplifying and manipulating the equation, there are contradictory statements or the variable disappears, leaving no possibility for the equation to hold true under any circumstances. This typically happens when attempting to solve the equation leads to a situation where no valid solution can be found that satisfies all conditions simultaneously.
How do you solve a linear equation with variables on both sides?
To solve a linear equation with variables on both sides, first simplify the equation by combining like terms on each side. Next, move all the variables to one side of the equation by performing inverse operations to isolate the variables. Once the variables are on one side and constants on the other, solve for the variable by performing the necessary operations to find its value. Finally, check your solution by plugging it back into the original equation to ensure it satisfies both sides of the equation.
What is the significance of the slope-intercept form of a linear equation?
The slope-intercept form of a linear equation, y = mx + b, is significant because it provides important information about the relationship between variables. The coefficient of x, m, represents the slope or rate of change of the line, indicating how much y changes for a one-unit change in x. The constant term, b, represents the y-intercept, which is the value of y when x is 0 and is also the point where the line intersects the y-axis. This form makes it easy to visualize and understand the behavior of a linear relationship, and it is commonly used in mathematics, science, and engineering for its simplicity and clarity.
Can a linear equation have infinite solutions? If so, how can you identify them?
Yes, a linear equation can have infinite solutions if the two sides of the equation represent the same line on a graph. In such cases, the equation is always true regardless of the value of the variables. One way to identify infinite solutions is if, when solving the equation, you end up with a statement like 0 = 0. This indicates that the equation holds true for any value of the variables, meaning it has infinite solutions.
What is the difference between solving a linear equation algebraically and graphically?
Solving a linear equation algebraically involves manipulating the equation using arithmetic operations to isolate the variable and find its value. On the other hand, solving a linear equation graphically involves plotting the equation on a coordinate plane and finding the intersection point(s) where the line crosses the x-axis, representing the solution(s) to the equation. Both methods ultimately provide the same solution, but offer different approaches to finding it.
What is the role of inverse operations in solving linear equations?
Inverse operations are fundamental in solving linear equations as they allow us to isolate the variable and find its value. By performing inverse operations, such as addition and subtraction, multiplication and division, on both sides of the equation, we can undo the operations that are applied to the variable. This process helps us to simplify the equation and eventually determine the value of the variable, thereby solving the linear equation.
How does the distributive property relate to solving linear equations?
The distributive property is crucial in solving linear equations because it allows us to simplify expressions by distributing a number to each term inside parentheses. This property helps us isolate the variable and solve for its value by combining like terms and manipulating the equation to isolate the variable on one side. By applying the distributive property correctly in the process of solving linear equations, we can efficiently move toward finding the solution for the unknown variable.
Can linear equations be solved using matrices? If so, explain the process.
Yes, linear equations can be solved using matrices through a method called matrix inversion. To solve a system of linear equations represented as AX=B, where A is the coefficient matrix, X is the variable matrix, and B is the constant matrix, you can find the inverse of matrix A (if it exists) and multiply it by the matrix B to find X. The formula for solving is X = A^-1 * B. This method is efficient for solving systems with multiple equations and variables.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.

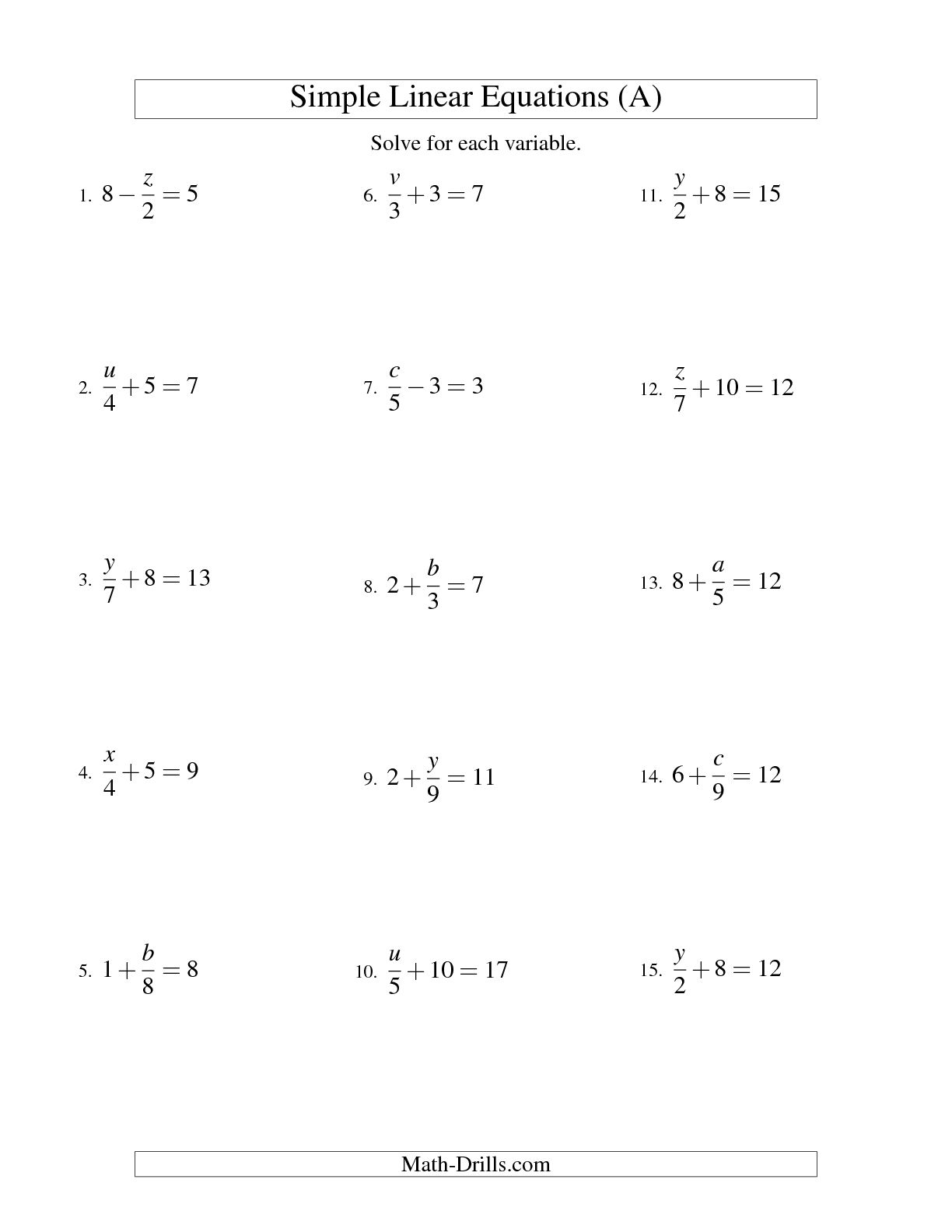





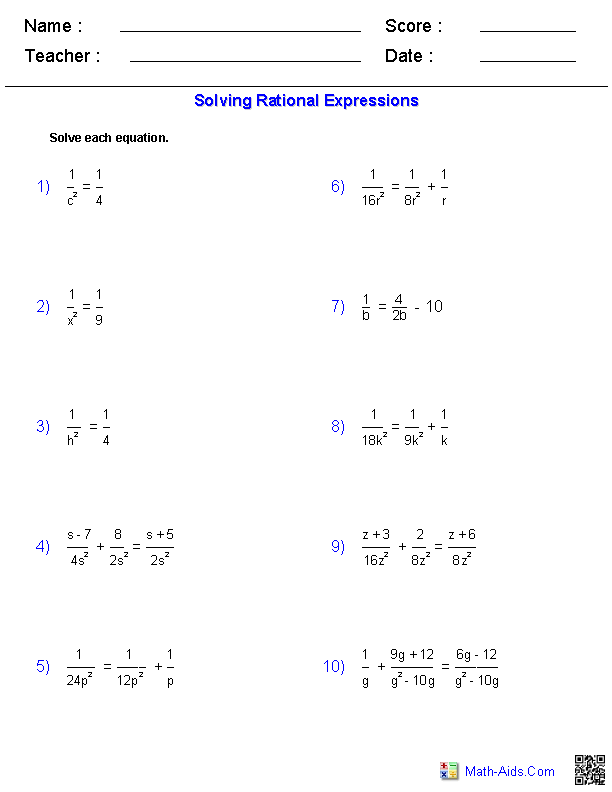

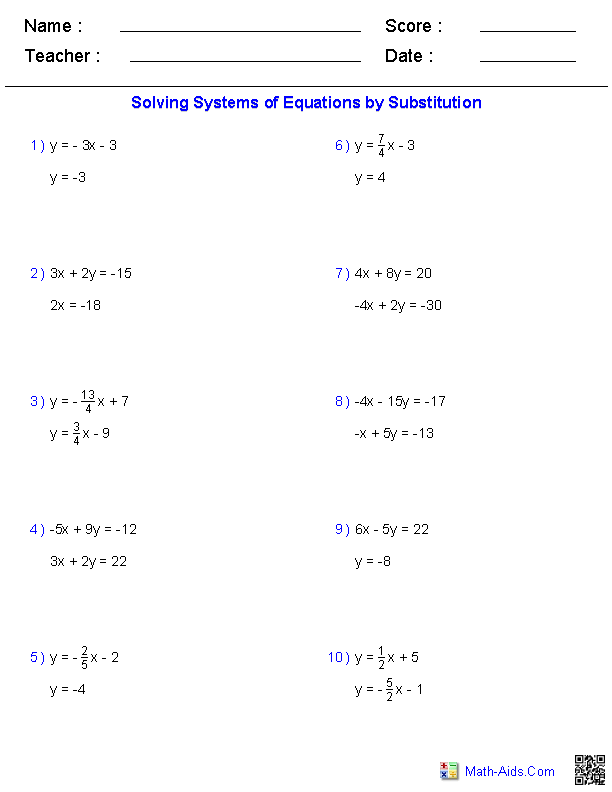





















Comments