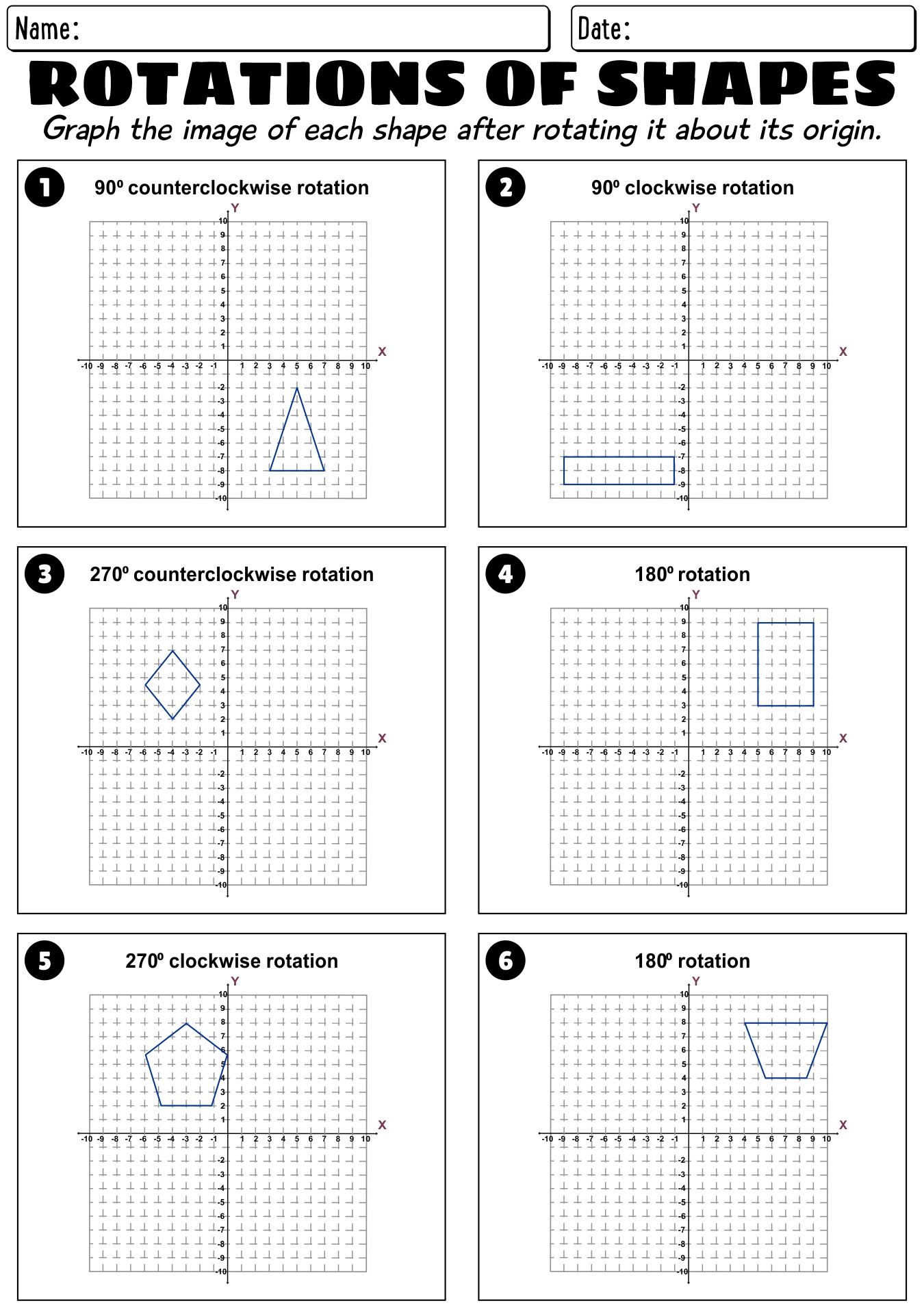
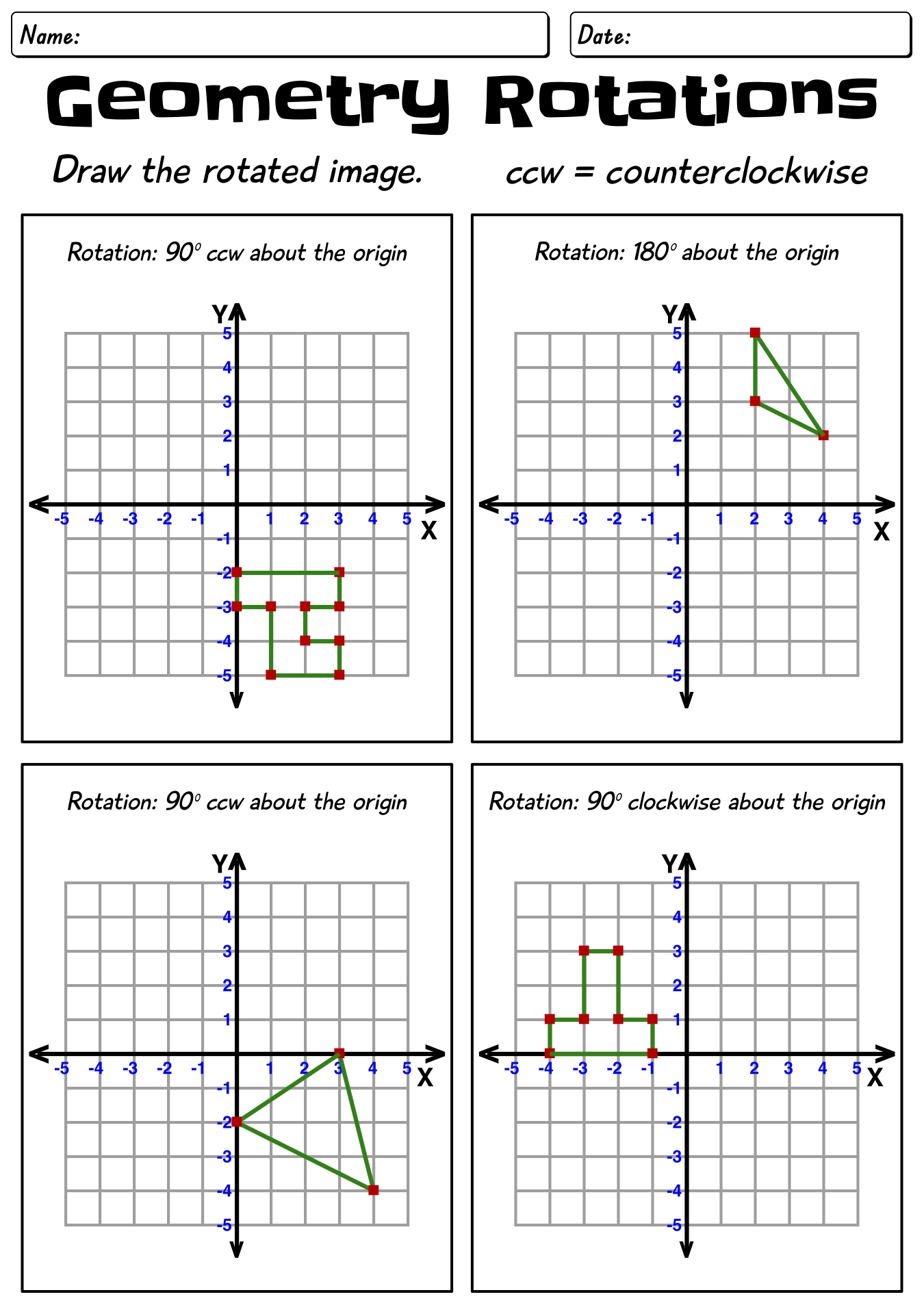
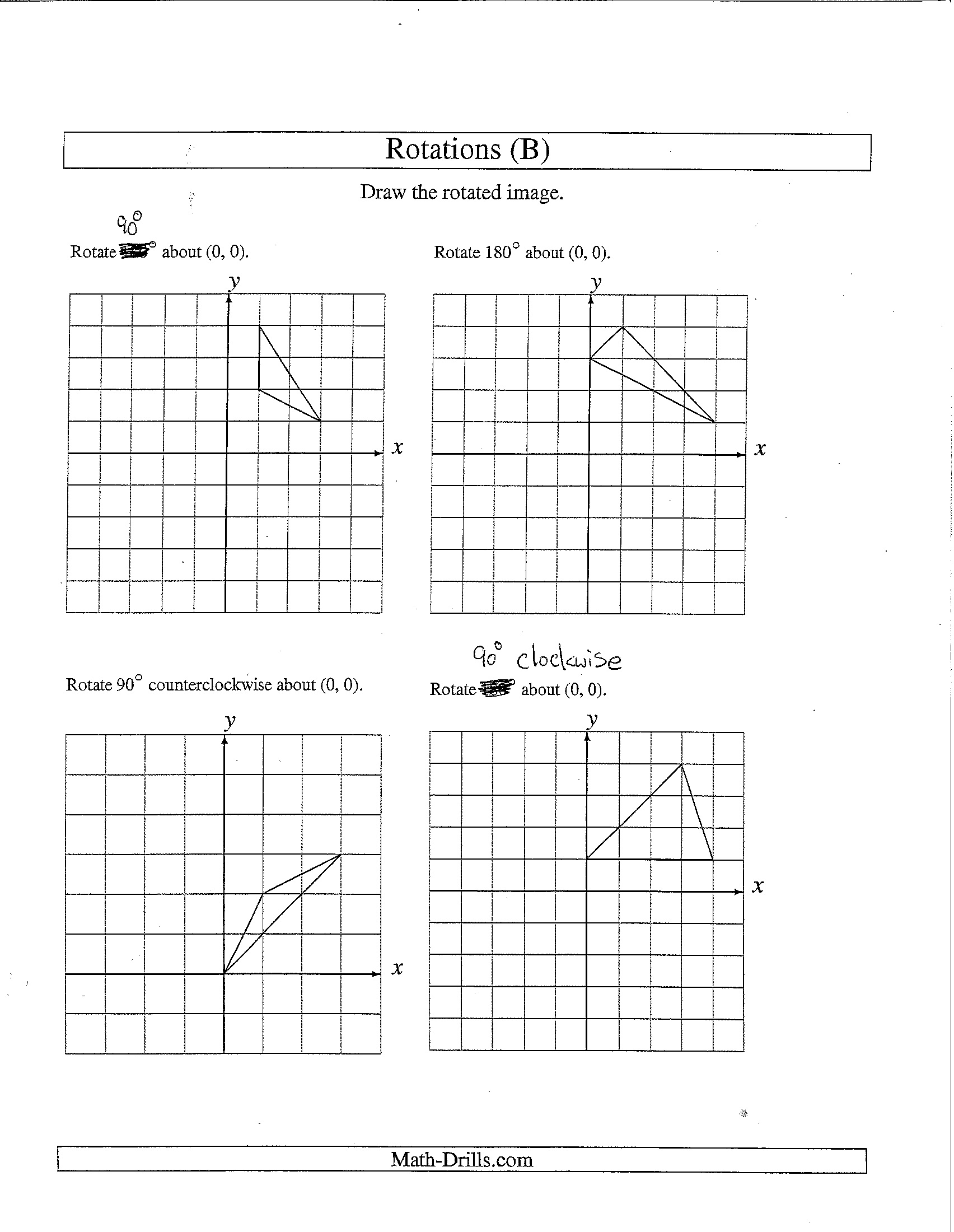
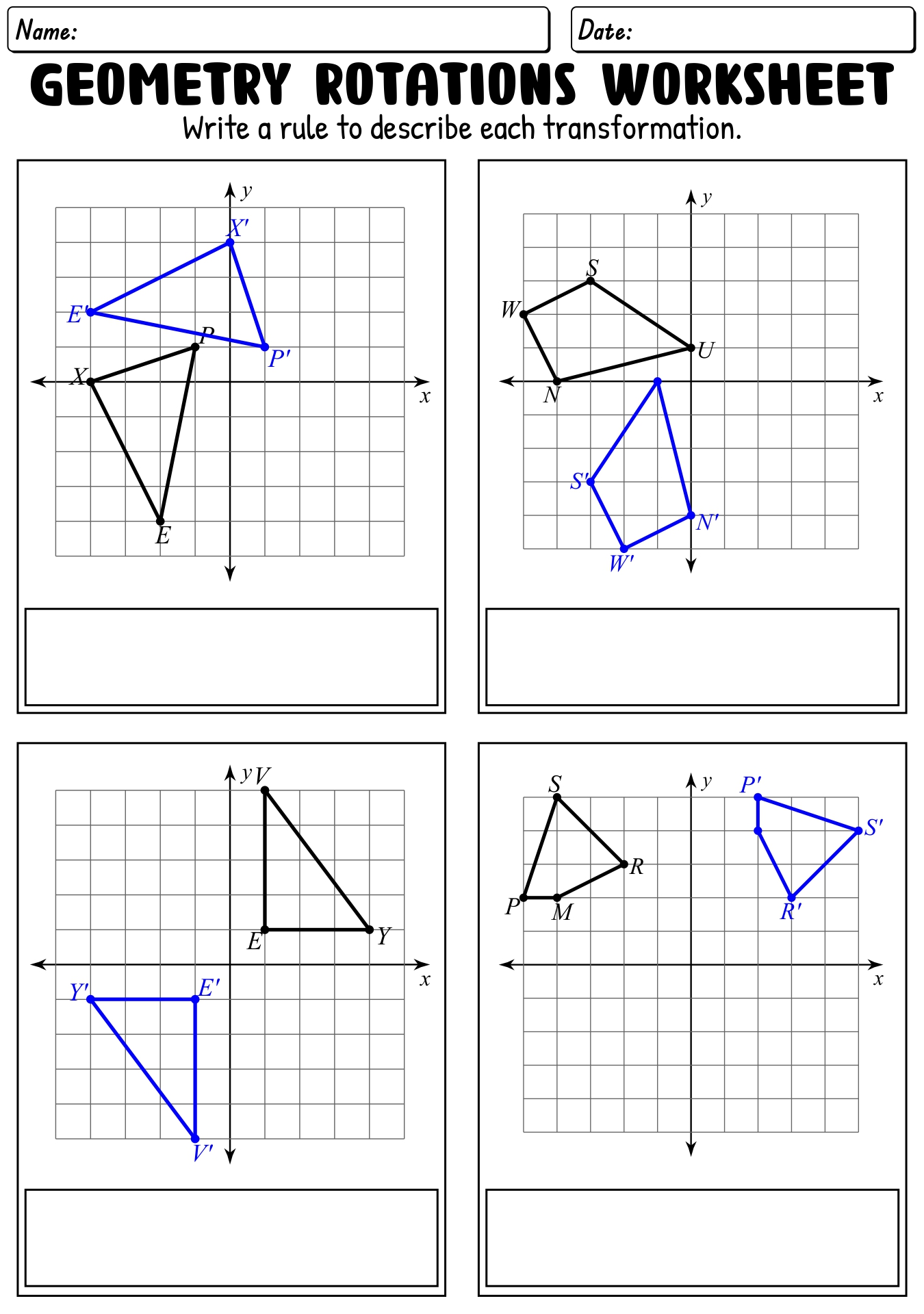
Rotations Worksheet 8th Grade
Are you an 8th grade student looking for a helpful tool to practice your knowledge of rotations? Look no further! Our Rotations Worksheet is here to assist you in understanding this important geometric transformation. With a focus on rotational symmetry and the properties of rotated figures, this worksheet will provide you with the perfect opportunity to enhance your skills in geometry.
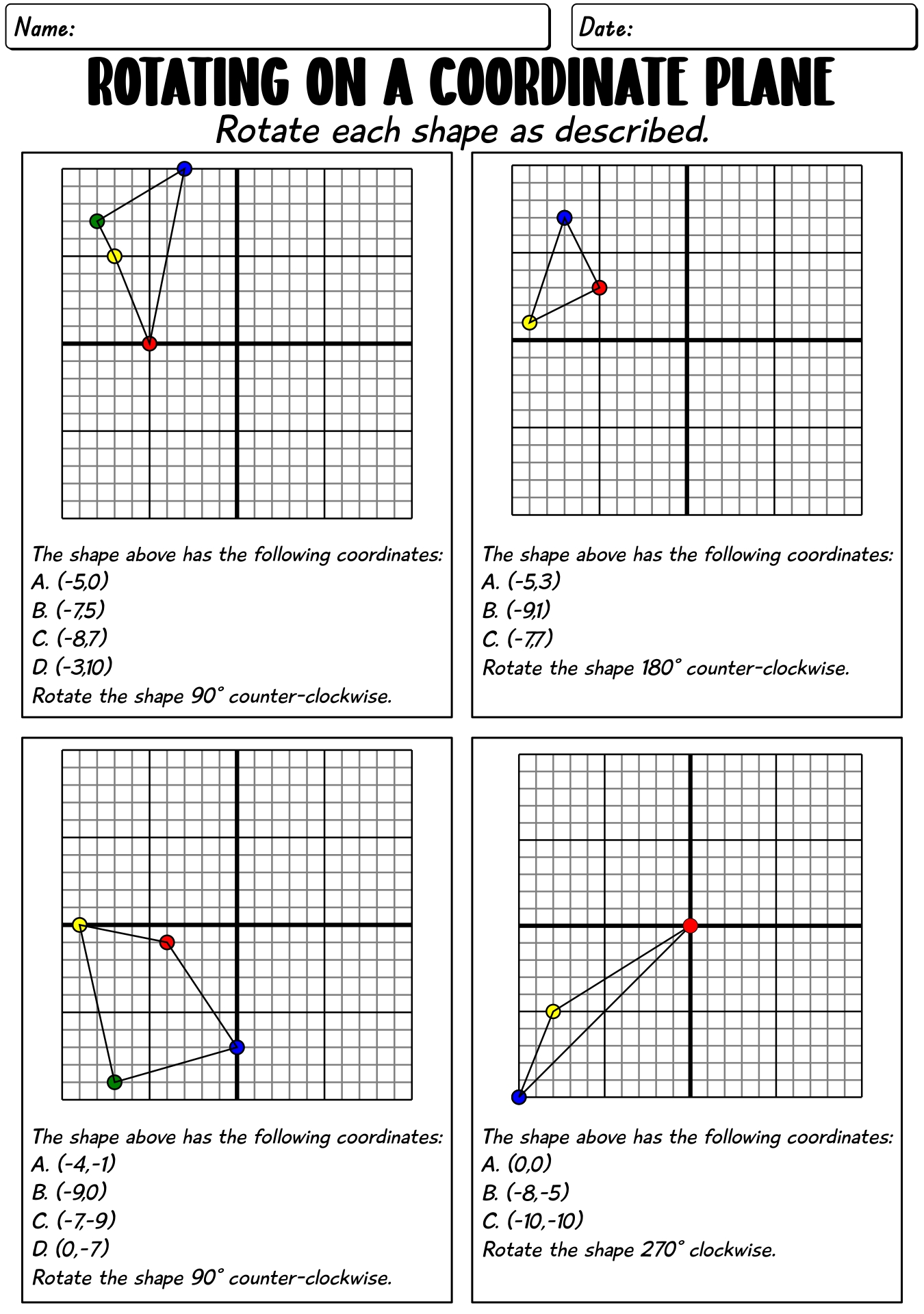
Table of Images 👆
- Geometry Rotations Worksheet
- Geometry Rotations Worksheet
- Rotation Worksheet 8th Grade Math
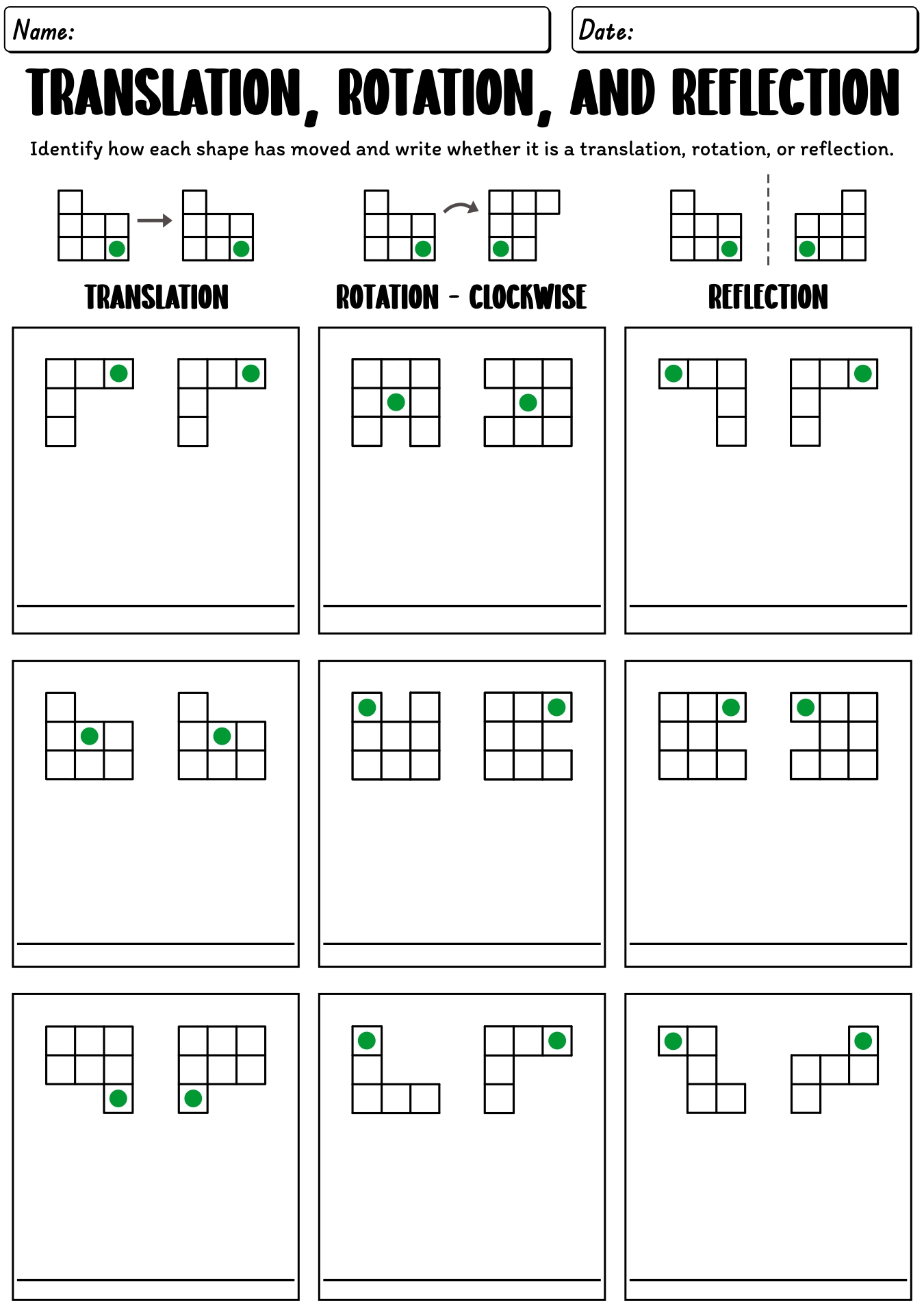
- Geometry Translation Reflection Rotation Worksheets
- Transformations Worksheets 8th Grade
- Transformation 8th Grade Math Worksheets
- Translation Reflection and Rotation Worksheets
- Geometry Rotations Worksheet
- Rotation Practice Worksheet
- Geometry Translations Worksheet
- Rotation Worksheet 8th Grade Math
- Geometry Rotations Worksheet
- Transformation Geometry Worksheets 8th Grade
- 8th Grade Math Rotations Practice Worksheets
- Geometry Rotations Activities for Grade 8
- Coordinate Plane Rotation Exercises Grade Eight

More 8th Grade Worksheets
8th Grade Spelling Worksheets8th Grade Worksheets Homeschooling
8th Grade Vocabulary Worksheets
Rotations Worksheet 8th Grade
What does a rotation in mathematics refer to?
In mathematics, a rotation refers to a transformation that turns a figure around a fixed point called the center of rotation. This transformation preserves the size of the figure and maintains the same overall shape, with every single point on the figure moving along a circular path by a certain angle around the center of rotation.
Describe how a point is rotated around a fixed point.
When a point is rotated around a fixed point, it means that the point moves in a circular path with the fixed point as its center. The rotation occurs by specifying an angle of rotation and then moving the point that many degrees or radians around the fixed point. This process creates a new position for the point based on the angle of rotation and the distance between the fixed point and the point being rotated.
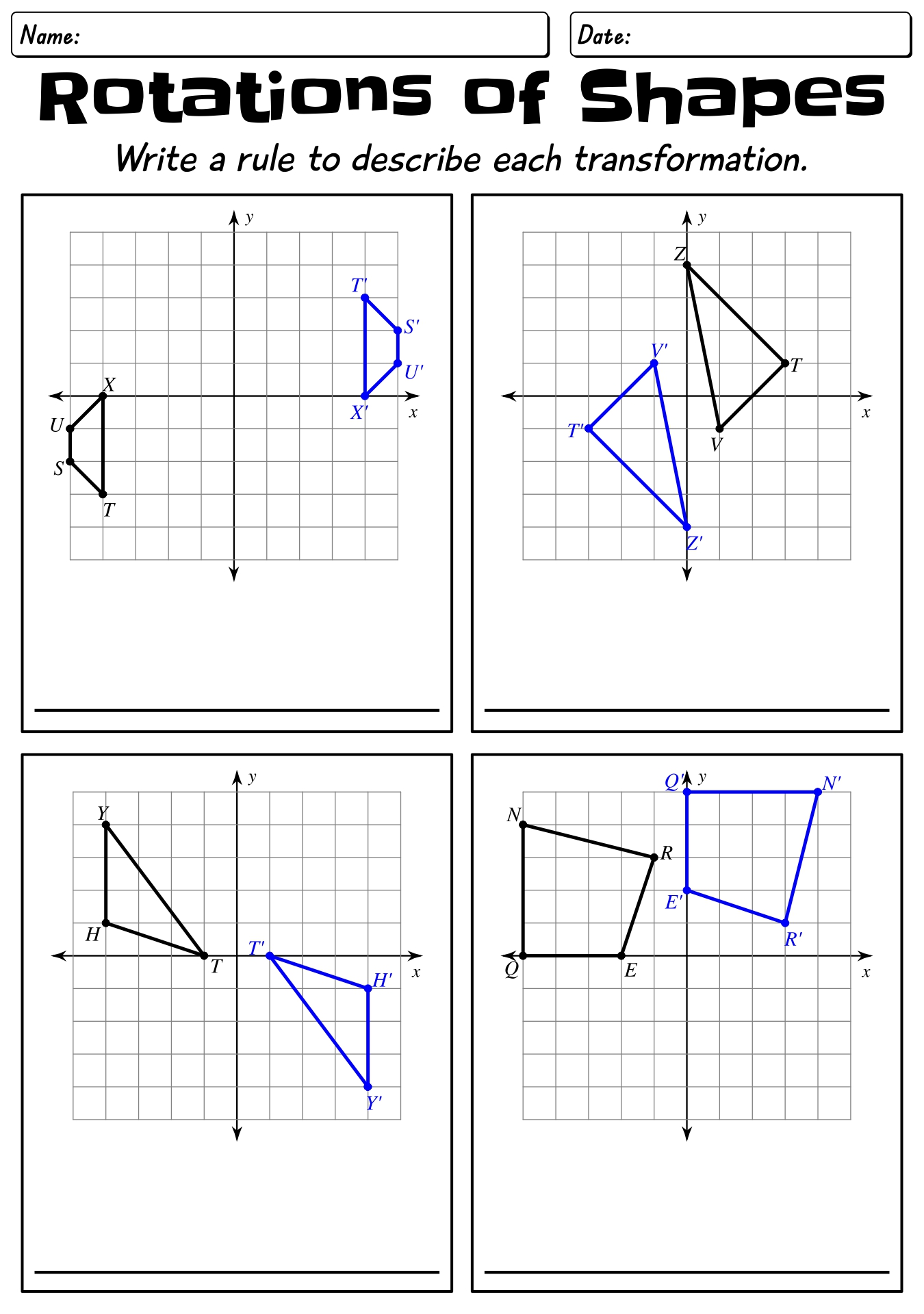
How is the rotation of an object described in terms of angles?
The rotation of an object is described in terms of angles by measuring the amount of rotation in degrees. One complete rotation around a point is equal to 360 degrees. The angle of rotation can be positive for counterclockwise rotation and negative for clockwise rotation. The measurement of angles helps to quantify and communicate the extent of rotation in a clear and standardized way.
Explain the difference between a clockwise rotation and a counterclockwise rotation.
In a clockwise rotation, an object turns in the direction in which the hands of a clock move, which is to the right. In contrast, a counterclockwise rotation involves movement in the opposite direction, to the left, as if going counter to the direction of the hands on a clock.
How can you determine the direction of a rotation from a given angle of rotation?
To determine the direction of a rotation from a given angle of rotation, you need to consider whether the rotation is clockwise or counterclockwise. In a standard coordinate system, rotations in a counterclockwise direction are considered positive, while rotations in a clockwise direction are negative. By knowing the sign of the angle of rotation (positive or negative), you can determine the direction of the rotation.
What is the relationship between the angle of rotation and the amount of turn?
The relationship between the angle of rotation and the amount of turn is direct and proportional. In other words, the more degrees an object or point rotates, the greater the amount of turn or change in direction it undergoes. For example, a 90-degree rotation corresponds to a quarter turn, a 180-degree rotation is a half turn, and a 360-degree rotation represents a full turn.
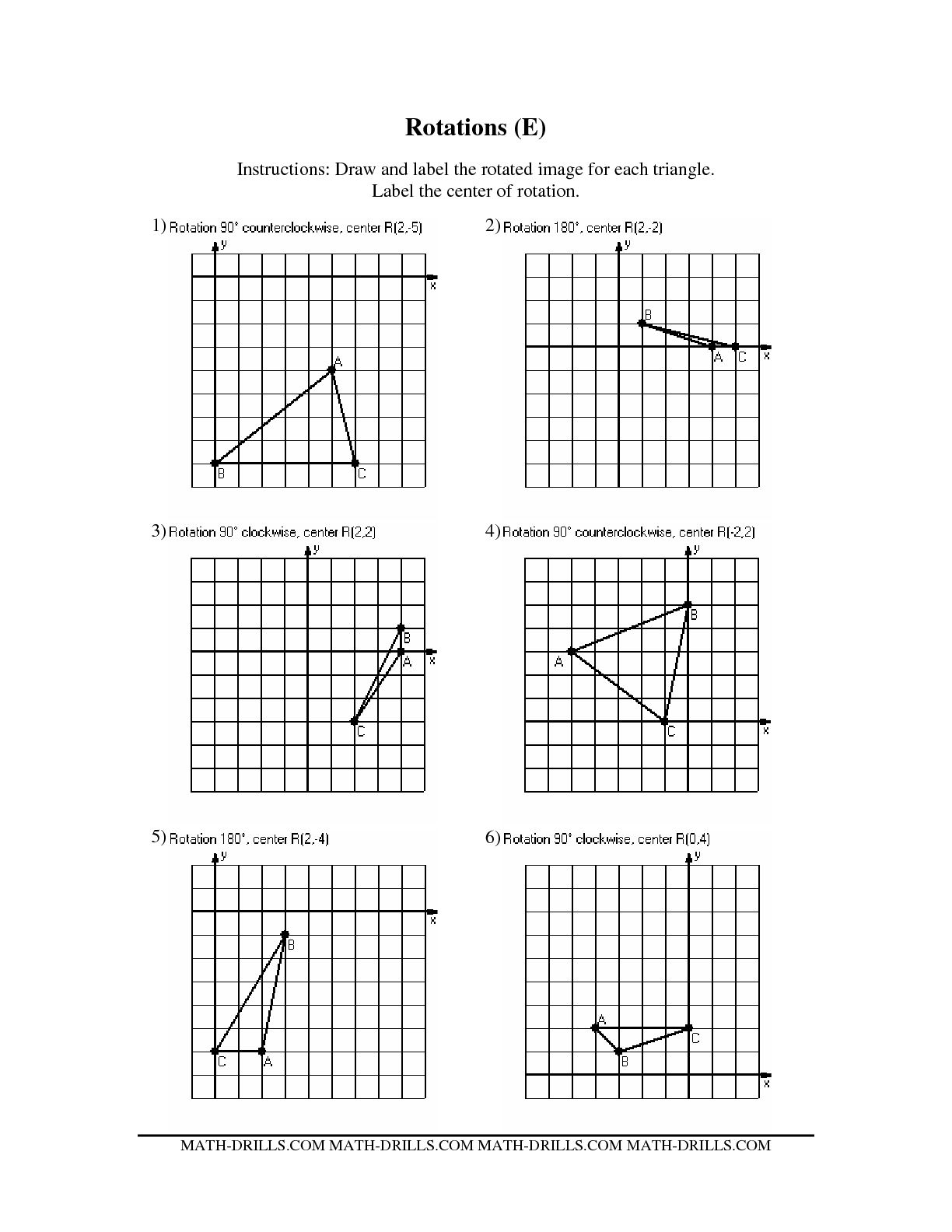
Describe the process of rotating a shape using a compass and protractor.
To rotate a shape using a compass and protractor, first, use the compass to draw a circle around the shape, making sure to mark the center point. Next, use the protractor to measure the desired angle of rotation from the center point. Place the protractor's center on the shape's center point and align the zero-degree mark with a reference point on the shape. Draw a line corresponding to the measured angle, and use it as a guide to rotate the shape by the specified amount. Finally, redraw the shape using the compass and protractor to reflect the rotated position accurately.
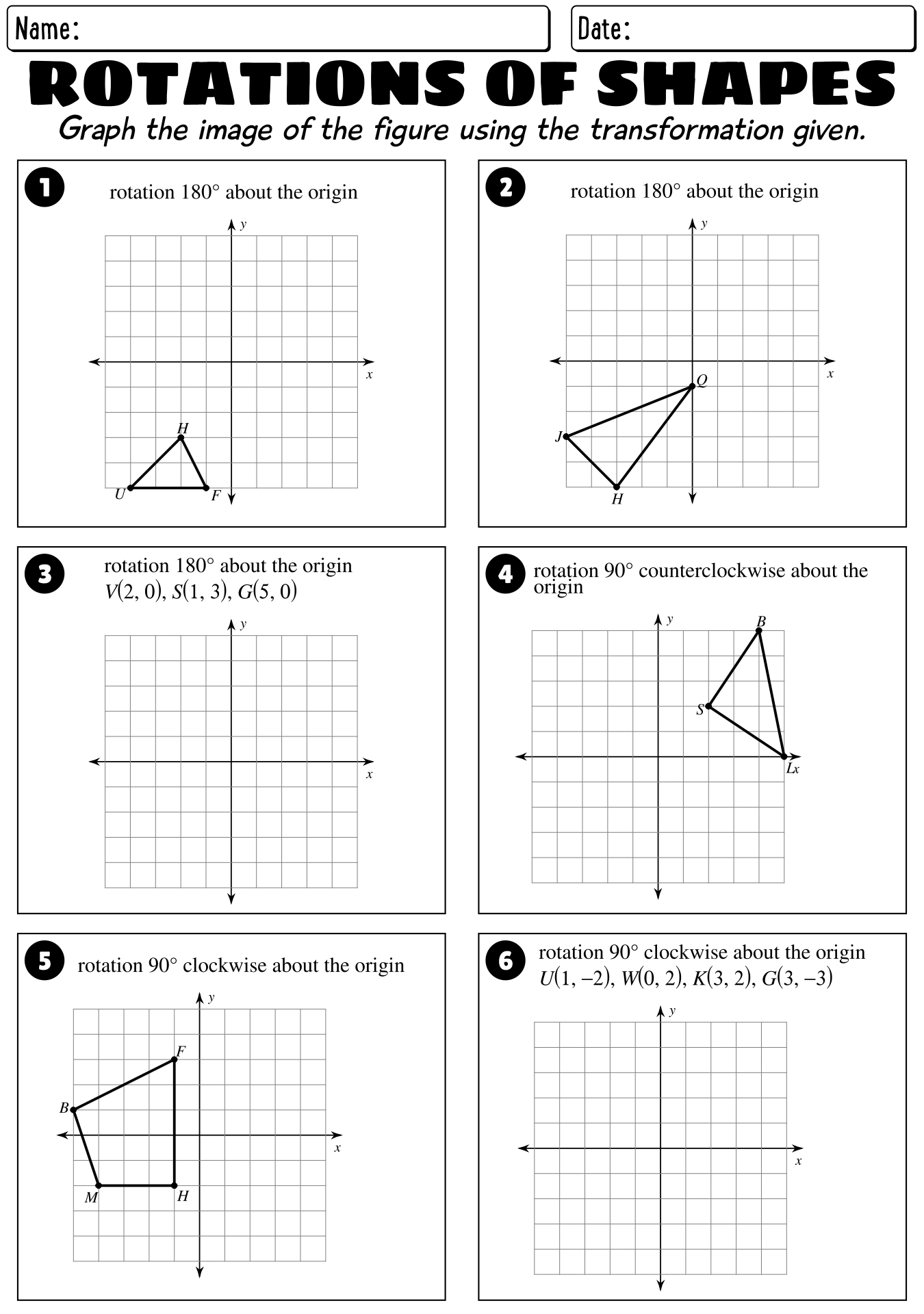
Explain how the coordinates of a point change after a rotation.
When a point is rotated around the origin, its new coordinates are determined by applying rotation formulas which involve trigonometric functions. The x-coordinate of the point is computed as x' = x*cos(?) - y*sin(?), while the y-coordinate is calculated as y' = x*sin(?) + y*cos(?), where (x,y) are the original coordinates of the point, ? is the angle of rotation, and (x',y') are the new coordinates after the rotation.
How can you determine the center of rotation based on the coordinates of the original and final positions of a point?
To determine the center of rotation based on the coordinates of the original and final positions of a point, you must first find the mid-point between the original and final positions. This mid-point represents the center of rotation. Calculate the average x-coordinate and the average y-coordinate separately to find the center of rotation in a Cartesian coordinate system.
Describe a real-life scenario where understanding rotations in mathematics would be useful.
Understanding rotations in mathematics would be useful in a scenario where you are a pilot navigating an aircraft. As a pilot, you would need to understand how to perform rotations to adjust the heading of the aircraft, make turns, and maintain the correct orientation in relation to the ground. This knowledge of rotations enables you to make precise adjustments and accurately navigate from one point to another, ensuring the safety and efficiency of the flight.
Have something to share?
Who is Worksheeto?
At Worksheeto, we are committed to delivering an extensive and varied portfolio of superior quality worksheets, designed to address the educational demands of students, educators, and parents.


















Comments