First Grade Fraction Worksheets

First-grade Fraction Worksheets provide a comprehensive and engaging way for young learners to develop a solid understanding of fractions. Designed specifically for first-grade students, these worksheets include various exercises and activities that introduce the concept of fractions in a clear and concise manner. With good visuals and age-appropriate content, these worksheets make learning about fractions enjoyable and accessible for first graders. By using these worksheets, 1st grade students will understand about main concepts of fractions such as fraction calculation, simplifying fractions, and equal fractions or equivalent fractions. Whether it's identifying parts of a whole or comparing fractions, these worksheets offer an effective tool to help young learners develop their understanding of fractions.

  15 Images of First Grade Fraction Worksheets

  First Grade Fractions Practice

---

  Shape Fractions Worksheets Grade 1

---

  Easter Egg Fractions Worksheet

---

  Fractions Halves Thirds Fourths Worksheet

---

  2nd Grade Fraction Worksheets

---

  Halves and Fourths Worksheets First Grade

---

  5th Grade Math Fraction Models Worksheets

---

  Quarters Fraction Worksheet First Grade

---

  Fractions and Equal Parts Worksheet

---

  Half and Quarter Fraction Worksheets

---

  2nd Grade Math Worksheets Fractions

---

  Printable 3rd Grade Math Worksheets Fractions

---

  Adding 3 Fractions Worksheets

---

  Printable 3rd Grade Math Worksheets Fractions

---

  Money and Fractions Worksheet

---

Enhancing early math skills can be fun with our first grade fraction worksheets, providing engaging ways to teach fractions.

Explore the mathematical world with these First Grade Fraction Worksheets!

What is Fraction in Math?

Fraction is one of the elements that students need to understand while learning math. It is a rational number in the form of in-line or ancient notation (a/b). The number a at the beginning (or top) is a numerator. Meanwhile, the b (or bottom) is a denominator.

According to the GCF (Goodwill Community Foundation) Global, the definition of fraction is a part of something whole and complete. It is less than the entire one thing; but more than zero (0).

Fraction might look intimidating. However, we use this mathematical element daily. Easy visualization of fractions would be using a pizza.

If you cut an entire pizza into eight (8) pieces and took one (1) slice, it would be 1/8 of the pizza. When the number of numerator and denominator are the same, it means the whole, or the same as one (1) (e.g. 3/3, 7/7).

What are The Types of Fraction?

According to the Central Bucks School District, there are three types of fractions in mathematics, proper, improper, and mixed.

• A proper fraction is a fraction with a numerator more than the denominator (e.g. 3/7, 6/10).
• An Improper fraction is a fraction with the numerator lesser than the denominator (e,g. 6/3, 8/2).
• An amixed fraction is a fraction that consists of one whole number and a proper fraction (e.g. 1 4/6, 7 5/9). The mixed reaction is always more than number one (1). 

We could change the improper to be a mixed fraction with the following steps:

1. Break the numerator with the denominator.
2. Take note of the complete number.
3. Write any residue number on the top of the denominator.

We could also convert the opposites (mixed fractions to improper fractions) with these steps:

1. Multiply the whole number by the denominator number.
2. Add the result to the numerator.
3. Write the final answer above the denominator.

Why Should Students Learn Fractions?

As one of the field topics in mathematics, fractions are essential subjects that students should master. Fraction is the basis of a more complicated mathematical formula, such as algebra.

According to Francis Fennel from the National Council of Teachers of Mathematics, many teachers wish their students to be skillful in fractions before the algebra class. Hence, the teacher needs to build a solid fraction base.

The ability to work with fractions is the essential foundation for students to learn more breakthrough mathematic topics. Francis said that fractions introduce abstract concepts to the students in the sense of mathematics.

How to Apply Fractions in The Real Life?

"Why do we learn this topic, though? We will never use this in real life." These types of responses might not be strange for mathematics teachers. It is not a surprise many students are struggling with mathematics, which is understandable.

For some of those students, mathematics is abstract knowledge. The teachers should help students notice how close mathematics in human life. Almost everything around us is related to math. Below are the real-life applications of fractions:

1. Splitting the bill with friends.
2. Divide meals with siblings.
3. Calculate the price of discounted stuff.
4. Recreate a food recipe.
5. Manage to take a well-balanced picture with a camera.
6. Count the time using a clock.
7. A Doctor makes prescriptions for medicine.

What are The Challenges in Teaching Fraction?

Every teacher might meet with challenges in their classroom. These disputes could come from the students, topic, strategy, mediums, and teacher themselves. In learning fractions, the students might struggle because they are not familiar with the form of the portion and a bunch of strange terms such as numerators, denominators, proper, improper, and more.

The teachers should find the roots of the problems and find the solution. The solution could be a change in learning strategy and medium, a four-eye discussion with students, and a talk with other mathematics teachers.

How to Teach Fraction?

Learning about fractions might be challenging for some students. Hence, the teachers should make a proper and suitable learning strategy to help the students understand the topic. These are some tips to teach fractions to students.

• Some education researchers recommend that teachers use real-life objects familiar to the students in teaching fractions. Use solid items such as stationery, snacks, toys, and more.
• You can ask the children to draw pictures of the item on the board to involve students in learning.
• When the students grasp the concept of fractions, the teacher can continue learning with rational numbers.
• In teaching fractions, the teacher should remember it takes a long time for the students to master this.
• Let the students absorb the concept and know all the elements.
• The teachers should find many teaching mediums to help the students understand fractions. The teacher can use visual helpers such as posters, flashcards, videos, or these First Grade Fraction Worksheets to aid the students.
  

What is included in the First Grade Fraction Worksheet?

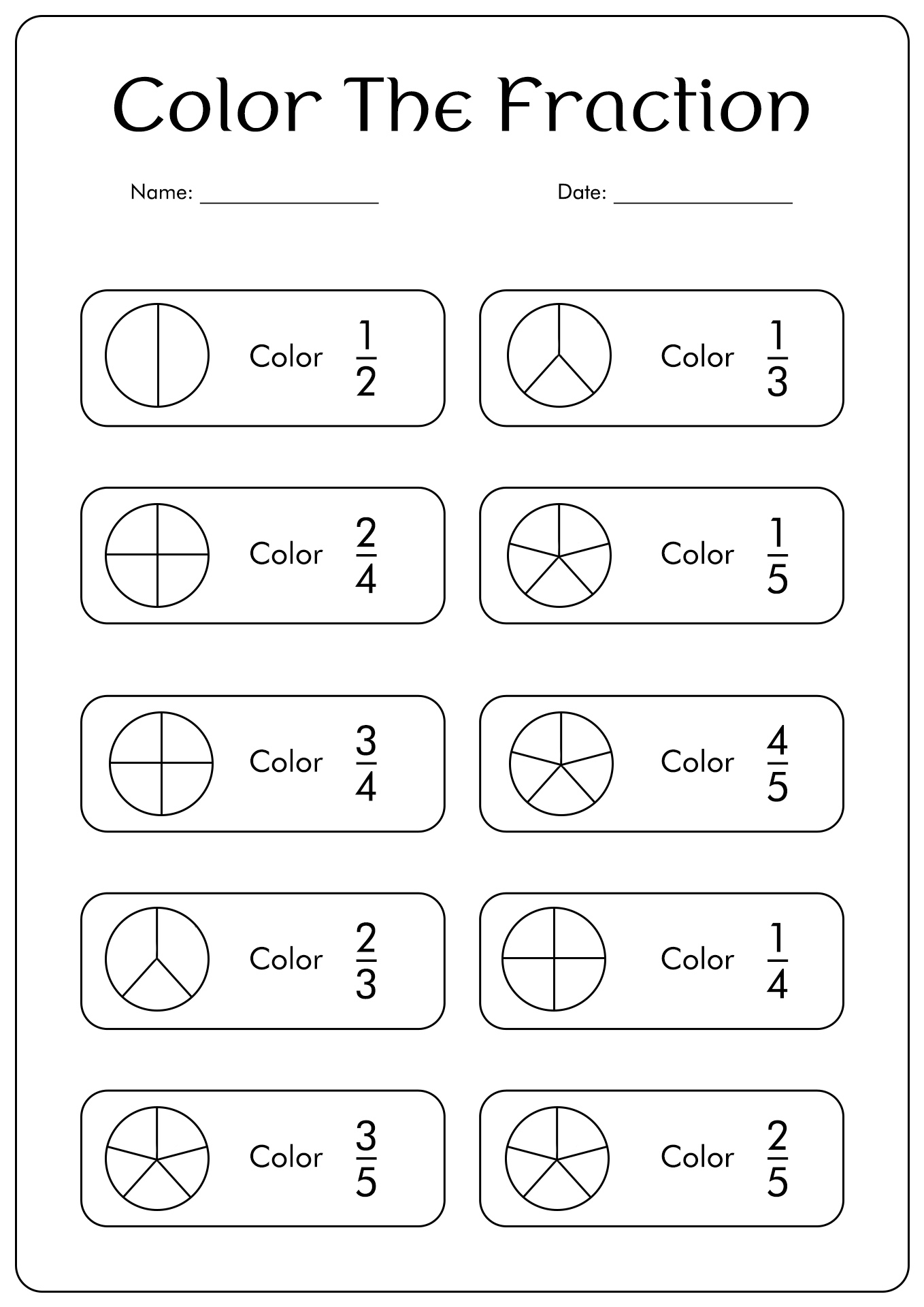
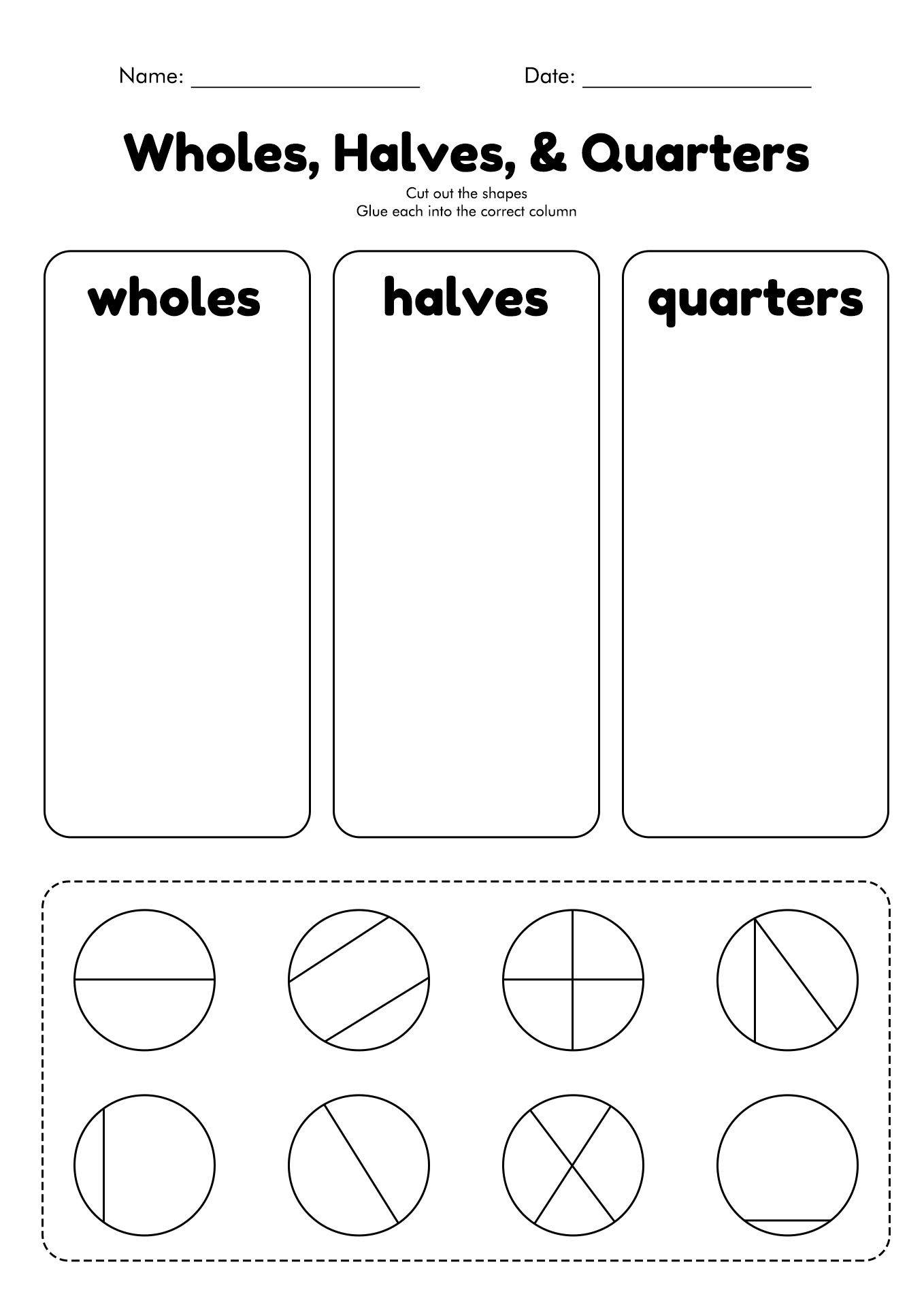
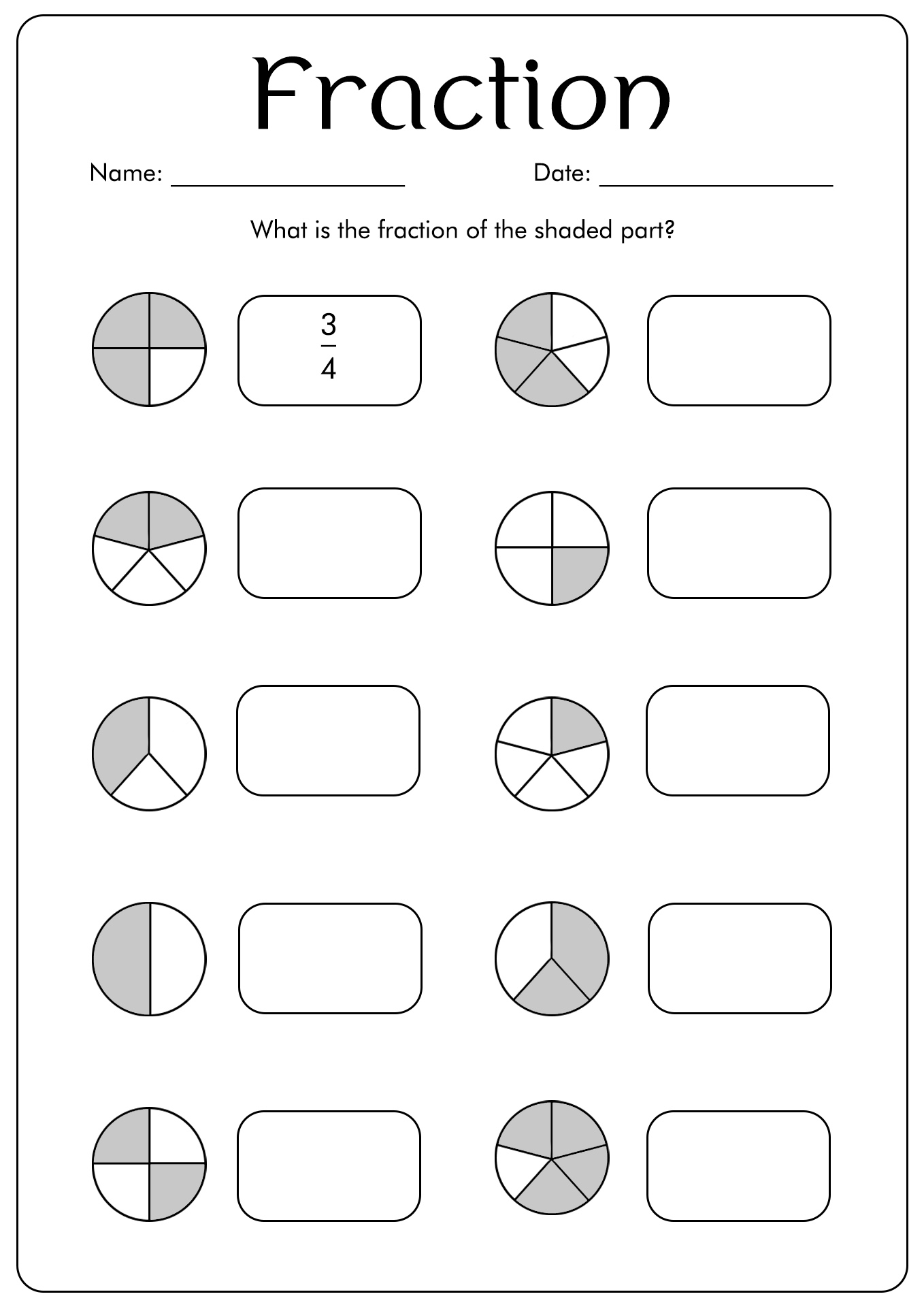
First Grade Fraction Worksheet is a worksheet designed for 1st grade students to help them understand about the main concept of fractions. These worksheets provide various simple shapes to learn fractions. 

An example is a square divided into four parts. So, students will understand how to write and read a fraction using that shape.

Teachers and parents can use First Grade Fraction Worksheets as a learning tool to teach fractions to 1st grade students in a fun way. These worksheets are easy to use. Teachers and parents just need to download and print our worksheets. Then, introduce and explain it to children.

Fraction is one of basic math concepts that should be learned by students, especially 1st grade students. Because fraction is important lesson, teachers and parents can use our First Grade Fraction Worksheets as the best tool to teach fraction to 1st grade students.

The ability to work with fractions (fraction addition, fraction subtraction, fraction multiplication, and fraction division) is the essential foundation for students to learn more breakthrough mathematic topics, such as algebra.